Ábrázoljuk az alábbi három függvényt a pozitív valós számok halmazán: x∈ℝ+!
|
|
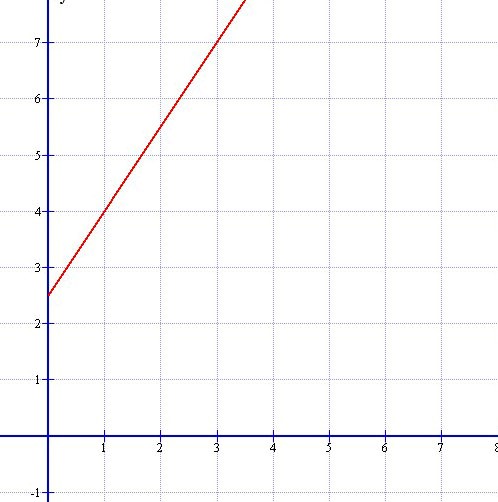
v(x)=1.5⋅x+2.5 |
|
Általánosabban:
a(x)=a
v(x)=a⋅x+k0
s(x)=ax2+k0⋅x
Fizikai jelentést is társíthatunk hozzájuk: (idő, út, sebesség, gyorsulás)
A gyorsulás időben állandó: a(t)=a.
Sebesség az idő függvényében: v(t)=at+k0.
Út az idő függvényében: s(t)=at2+k0⋅t.
Milyen kapcsolatot fedezhetünk fel a fenti függvények között?
(v(t))’= a(t)
(s(t))’= v(t)
Mi a kapcsolat az alábbi függvények között?
f(x)=3 és F(x)=3x között?
f(x)=3 és F(x)=3x-2 között?
f(x)=3x2 és F(x)=x3 között?
f(x)=3x2 és F(x)=x3+5 között?
f(x)=cosx és F(x)=sinx+C között?
f(x)=F’(x)
Definíció:
Legyen f(x) az [a;b] intervallumon értelmezve. Ha létezik az f(x) függvényhez olyan [a;b] intervallumon értelmezett F(x) függvény, hogy minden x∈ [a;b]-re F’(x)=f(x) akkor azt mondjuk, hogy az F(x) függvény az f(x) függvény primitív függvénye (antideriváltja).
A fenti definíció közvetlen következménye:
Tétel:
Ha F(x) függvény primitív függvénye f(x) függvénynek, akkor az F(x)+c függvény is primitív függvénye az f(x) függvénynek, ahol c∈ℝ konstans.
Tehát, ha egy f(x) függvénynek van primitív függvénye, akkor f(x) függvénynek végtelen sok primitív függvénye van, amelyek csak egy konstansban térnek el egymástól.
Az alábbiakban nézzük néhány alapvető függvény primitív függvényét!
Az f(x)=xn függvény primitív függvénye: \( F(x)=\frac{x^{n+1}}{n+1}+c \), mert F'(x)=f(x).
Az \( f(x)=\sqrt{x} \) függvény primitív függvénye:\( F(x)=\frac{2}{3}x^{\frac{3}{2}}=\frac{2}{3}\sqrt{x^{3}}=\frac{2}{3}x\sqrt{x} +c\), mert F'(x)=f(x).
Az f(x)=cos(x) primitív függvénye F(x)=sin(x)+c, mert sin(x)’=cos(x), azaz F'(x)=f(x).
Az f(x)=sin(x) függvény primitív függvénye:F(x)=-cos(x)+c, mert cos(x)’=-sin(x), azaz F'(x)=f(x).
A primitív-függvény keresés a differenciálás megfordításaként fogható fel.
Megjegyzés: Nincs minden függvénynek primitív függvénye. Bizonyítható például, hogy az \( f(x)=\left\{ \begin{array}{} 1 & ha \; x≥0 \\ 0 & ha \; x<0 \\ \end{array} \right\} \) függvénynek nincs primitív függvénye.
Ugyanakkor be lehet bizonyítani a következő tételt:
Tétel:
Ha az f(x) függvény folytonos egy [a;b] intervallumon, akkor ezen az [a;b] intervallumon az f(x) függvénynek van primitív függvénye.
Definíció:
Az f(x) függvény primitív függvényeinek összességét (halmazát) az f(x) függvény határozatlan integráljának nevezzük és az \( \int{f(x)}dx \) szimbólummal jelöljük.
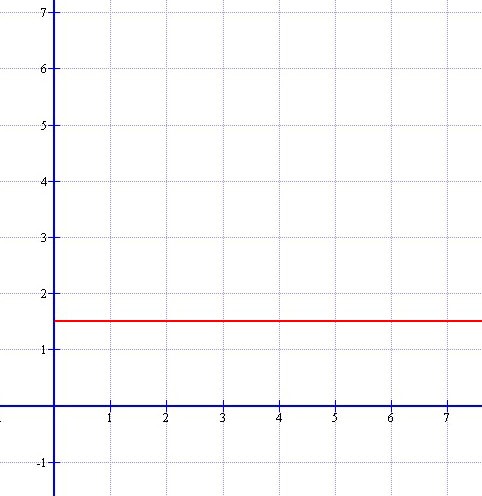 a(x)=1.5
a(x)=1.5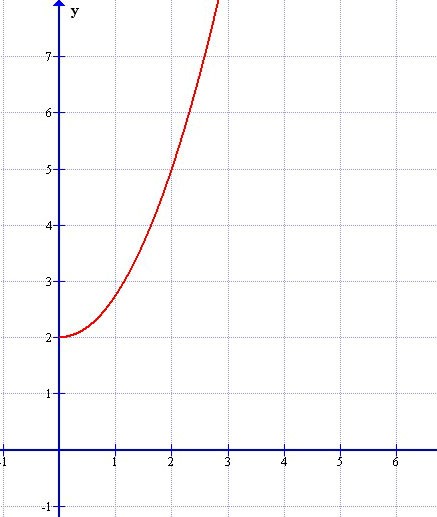 s(x)=0.75⋅x2+2.5⋅x
s(x)=0.75⋅x2+2.5⋅x

Comments are closed, but trackbacks and pingbacks are open.