Pitagoraszi számhármasok

Definíció:

Pitagoraszi számhármason három olyan pozitív egész szám együttesét értjük, amelyek kielégítik az x²+y²=z² egyenletet. x;y;z∈ℤ.

Ennek a speciális diophantoszi egyenletnek nyilvánvaló megoldása például x=3, y=4 és z=5.

A pitagoraszi számhármasokkal mint oldalhosszúságokkal szerkesztett háromszögek mindig derékszögűek lesznek, hiszen megfelelnek Pitagorasz tételének.

Természetesen egy számhármas pozitív egész számú többszöröse is pitagoraszi számhármas. Így például a 6, 8, 10.
A nagyobb számok között azonban egyre ritkábbak azok a pitagoraszi számhármas, amelyek ne lennének valamelyik kisebb számhármas többszörösei.

A pitagoraszi számhármasok előállítási módját Pitagorasz követői, a püthagoreusok találták meg.

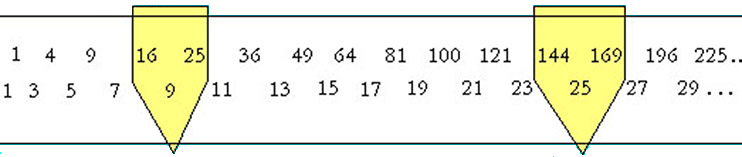
A felső sorban a négyzetszámok, az alsó sorban pedig a páratlan számok vannak. Az alsó sorban található négyzetszám a felső sorban a „felette” lévő két négyzetszámmal együtt pitagoraszi számhármast alkot.

Azt hogy végtelen sok ilyen számhármas van, Eukleidész bizonyította be először.

Az alábbi formulával pitagoraszi számhármasokat tudunk előállítani:
(m²-n²)²+(2mn)²=(m²+n²)². Itt m és n tetszőleges pozitív egész számok, ahol m>n.

Ha azt akarjuk, hogy a kapott számhármasok „függetlenek” legyenek, azaz ne legyenek egy kisebb számhármas többszörösei, akkor az m és n változókra a következő kikötést kell tenni:

1. Az m és n számok különböző paritásúaknak kell lenniük. (egyik páros, másik páratlan.)
2. Relatív prímek legyenek, azaz (m,n)=1

Egy pár példa:

m	n	x	y	z	x2	y2	z2
2	1	3	4	5	9	16	25
3	2	5	12	13	25	144	169
4	3	7	24	25	49	576	625
4	1	15	8	17	225	64	289
5	4	9	40	41	81	1600	1681

A pitagoraszi számhármasokkal már a babilóniai régészeti leleteken is találkozhatunk, és az ókori egyiptomiak és kínaiak is ismerték, mint tapasztalati tényt.

A pitagoraszi számhármasok kapcsán viszonylag hamar felvetődött a kérdés, hogy van-e ennek „térbeli megfelelője”, azaz vannak-e olyan pozitív egész számok, amelyekre az x³+y³=z³ összefüggés igaz.

Vagyis lehet-e két darab egységnyi oldalú építőkockákból álló kockából kirakni egy harmadik kockát. Ha például megpróbálunk egy 6, illetve 8 egységnyi oldalhosszúságú kockákból összerakni egyet, akkor tudunk ugyan egy 9 oldalhosszúságú „kockát” építeni, de egy kis kocka hiányozni fog:
6³+8³=9³-1.

Később még általánosabban fogalmazták meg a problémát, és keresték az xⁿ+yⁿ=zⁿ egyenlet megoldásait, ahol x, y, z pozitív egész számok és n>2.

Fermat volt az aki először leírta, hogy ennek a feladatnak nincs megoldása, és ezt a feljegyzése szerint be is tudja bizonyítani. Ezt a bizonyítását azonban soha nem írta le. Így maradt rajta a név: Fermat sejtés. Csak 1993-ban sikerült Andrew Wiles-nak, egy angol matematikusnak a tétel bizonyítása.