Paralelogramma, trapéz illetve háromszög középvonala

Definíció: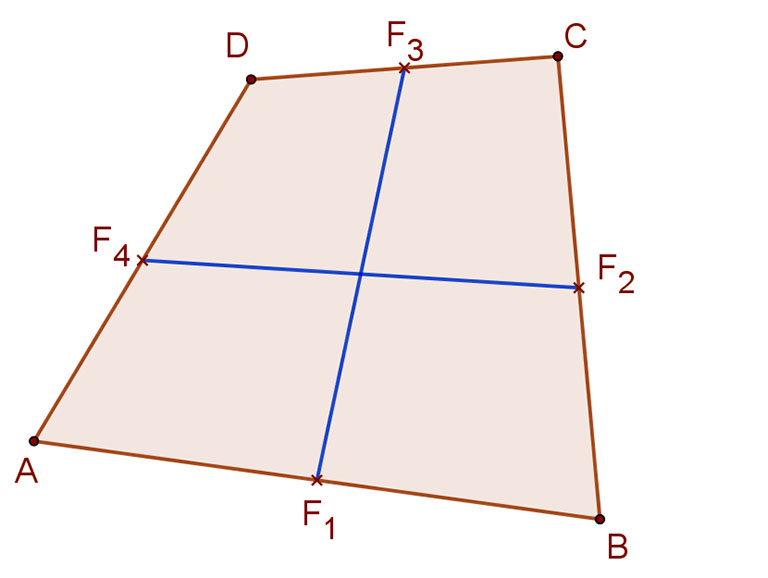

A négyszög szemközti oldalainak felezési pontját összekötő szakaszokat a négyszög középvonalának nevezzük.
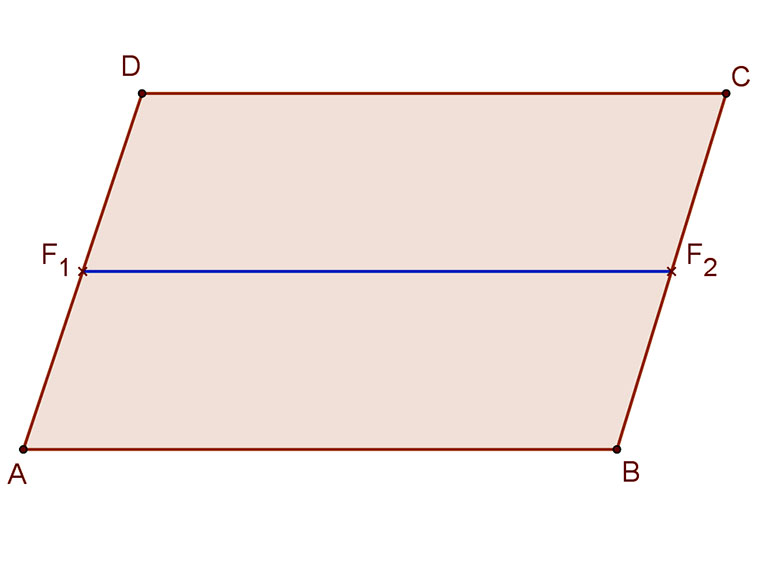
A mellékelt ábra szerint az ABCD négyszög középvonalai az F₁F₃ és az F₂F₄ szakaszok.

Paralelogramma középvonala

Tétel:

A paralelogramma két szemközti oldalának felezőpontját összekötő középvonala párhuzamos és egyenlő hosszúságú a másik két oldallal.

A mellékelt ábra jelölései szerint:
F₁F₂||AB||DC és F₁F₂=AB=DC.

 Bizonyítás:

Mivel AD||BC és AD=BC, ezért AF₁||BF₂ és AF₁=BF₂, tehát az ABF₁F₂ és a F₁F₂CD négyszögek paralelogramma.
Ezért F₁F₂||AB||DC és F₁F₂=AB=DC.

Trapéz középvonala:

Definíció:

A trapéz olyan négyszög, amelyeknek van két párhuzamos oldala. A másik két oldalt a trapéz szárainak mondjuk.

Tétel: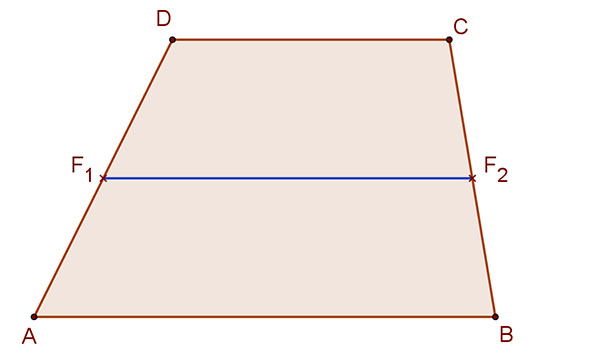

A trapéz két szárának felezési pontjait összekötő középvonala párhuzamos a trapéz párhuzamos oldalaival, és hossza a párhuzamos oldalak hosszának számtani közepe. 

A mellékelt ábra jelölései szerint:
F₁F₂||AB||CD és ​\( F_{1}F_{2}=\frac{AB+CD}{2} \)​.

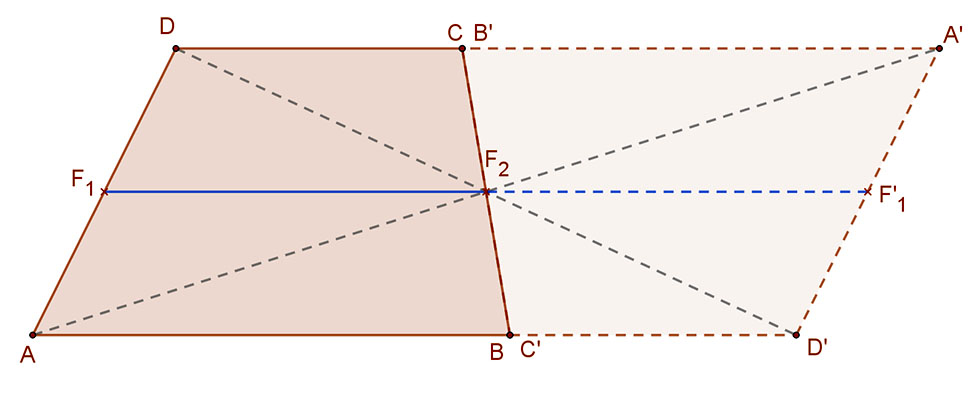Bizonyítás:

Tükrözzük a trapézt az egyik szár felezési pontjára. (Az ábrán az F₂-re). A tükrözés következtében paralelogrammát kapunk. (az AD’A’D) Ennek a paralelogrammának az AD’ és A’D oldalai a trapéz párhuzamos oldalainak összegével egyenlő. AZ AD’A’D paralelogrammában F₁F’₁=AD’=AB+DC. Másrészt F₁F’₁=2F₁F₂. Így a fenti állítást kaptuk: \( F_{1}F_{2}=\frac{AB+CD}{2} \)​.

Háromszög középvonala:

Definíció:

A háromszög középvonala a háromszög két oldalának felezési pontját összekötő szakasz.

Tétel: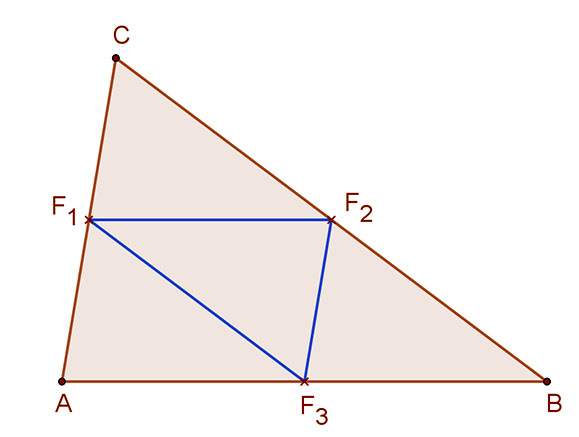

A háromszög bármelyik középvonala párhuzamos a harmadik oldallal és a középvonal hossza fele a harmadik oldal hosszának.

A mellékelt ábra jelölései szerint:
F₁F₂||AB és 2F₁F₂=AB
F₁F₃||BC és 2F₁F₃=BC
F₃F₂||AC és 2F₃F₂=AC.

Bizonyítás:

Azt akarjuk igazolni, hogy F₁F₂||AB és 2F₁F₂=AB.

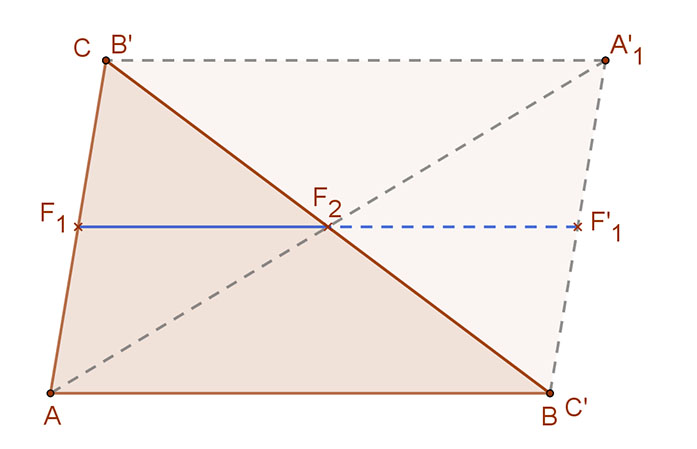Tükrözzük a háromszöget az egyik, jelen esetben az F₂ felezési pontjára. Mivel F₂ felezési pont, a B és C pontok egymás tükörképei. A tükrözés következtében az AC szakasz képe az BA’ szakasz, az AB szakasz képe pedig a CA’ szakasz lesz, és AC||BA’, AB||CA’.
Így tehát az ABC háromszögből az ABA’C paralelogrammát kaptuk. Ennek középvonala F₁F’₁, és a tükrözés következtében F₁F₂ =F₂F’₁, tehát 2F₁F₂=F₁F’₁.

A paralelogramma középvonala párhuzamos és egyenlő a szembelévő oldallal, ezért F₁F’₁||AB, és F₁F’₁=AB.
Tehát F₁F₂||AB, és 2F₁F₂=AB.

És ezt kellett bizonyítani.

Tétel:

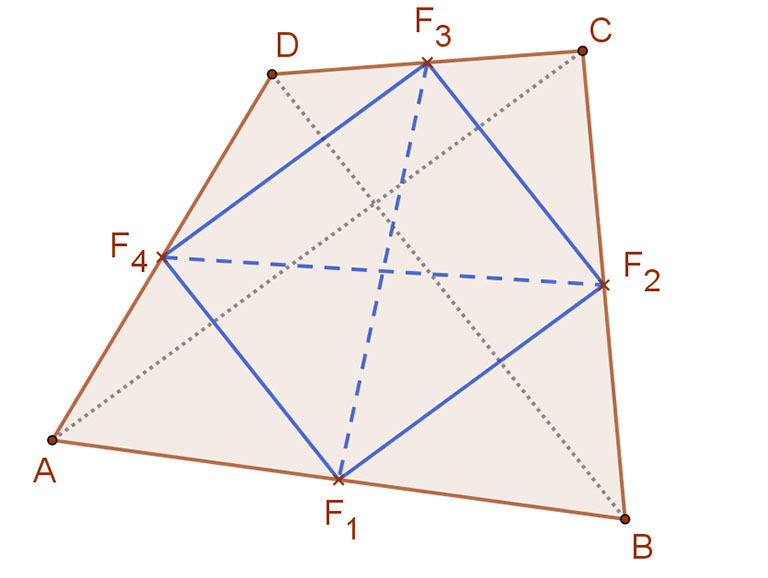
A négyszögek oldalfelező pontjai egy paralelogrammát határoznak meg.

Az állítás szerint a mellékelt ábrán az ABCD négyszögben F₁F₂F₃F₄ paralelogramma.

Bizonyítás:

Mivel a négyszög F₁F₂ középvonala az ABC háromszögnek is középvonala, ezért F₁F₂||AC és 2F₁F₂=AC.

Ugyanígy a négyszög F₄F₃ középvonala az ACD háromszögnek is középvonala, ezért F₄F₃||AC és 2F₄F₃=AC. Így tehát F₄F₃||F₁F₂ és F₄F₃=F₁F₂.

Tehát az F₁F₂F₃F₄ oldalfelezési pontok által meghatározott négyszög paralelogramma.

Feladat:

Egy síknégyszög oldalfelező pontjai rombuszt alkotnak.
Mi állítható e négyszögről?

(Összefoglaló feladatgyűjtemény 1738. feladat.)

Megoldás:

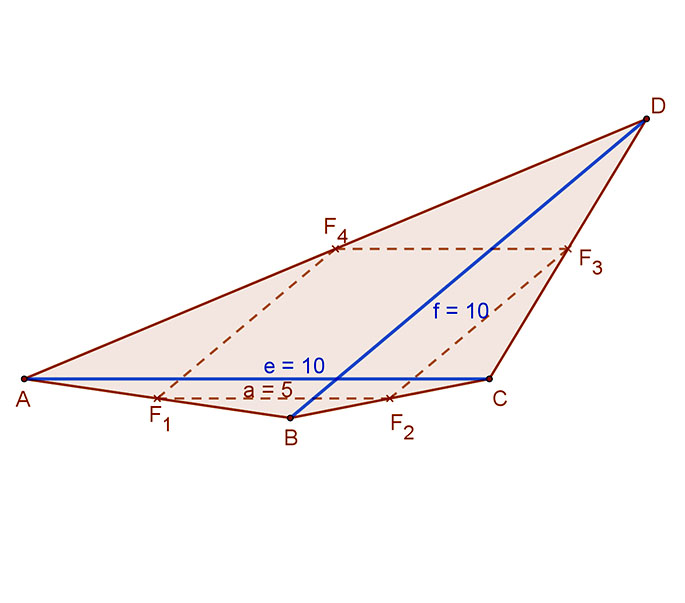A négyszög középvonala párhuzamos a négyszög átlójával és hossza az átló fele. A mellékelt ábra jelölései szerint: 2F₁F₄=BD és 2F₁F₂=AC.
Mivel a középvonalak egy rombusz oldalai, ezért egymással egyenlők, következésképpen a négyszög átlói is egyenlők. Azaz mivel F₁F₄=F₁F₂, ezért AC=BD.

A válasz tehát: Az ilyen négyszögek átlói egyenlő hosszúságúak.