Napóleon háromszögek

Tétel: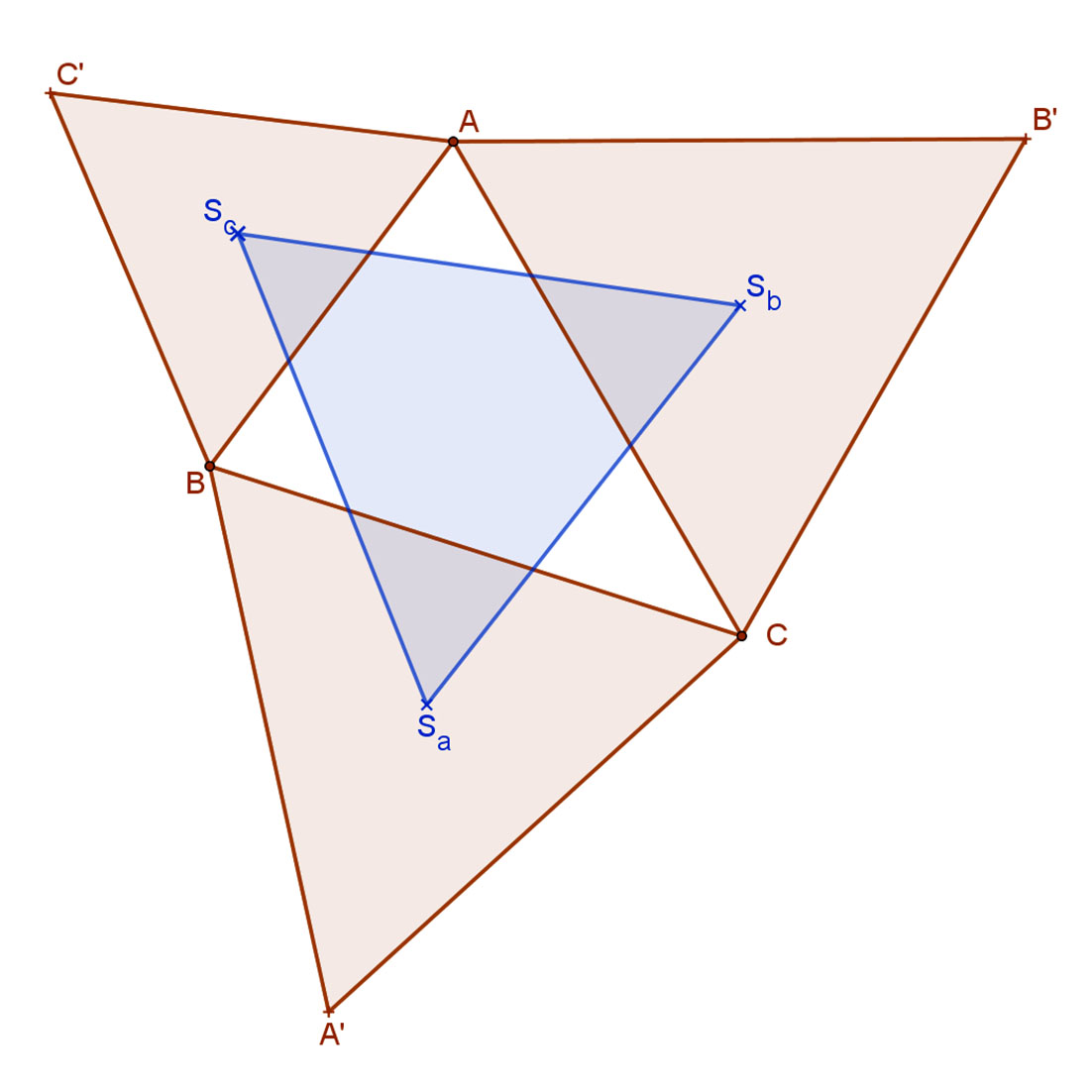

Ha az ABC háromszög oldalaira kifelé emelünk egy-egy szabályos háromszöget, akkor ezen szabályos háromszögek középpontjai mindig szabályos háromszöget alkotnak.  Ezt a szabályos háromszöget az eredeti háromszög külső Napóleon-háromszögének nevezzük.

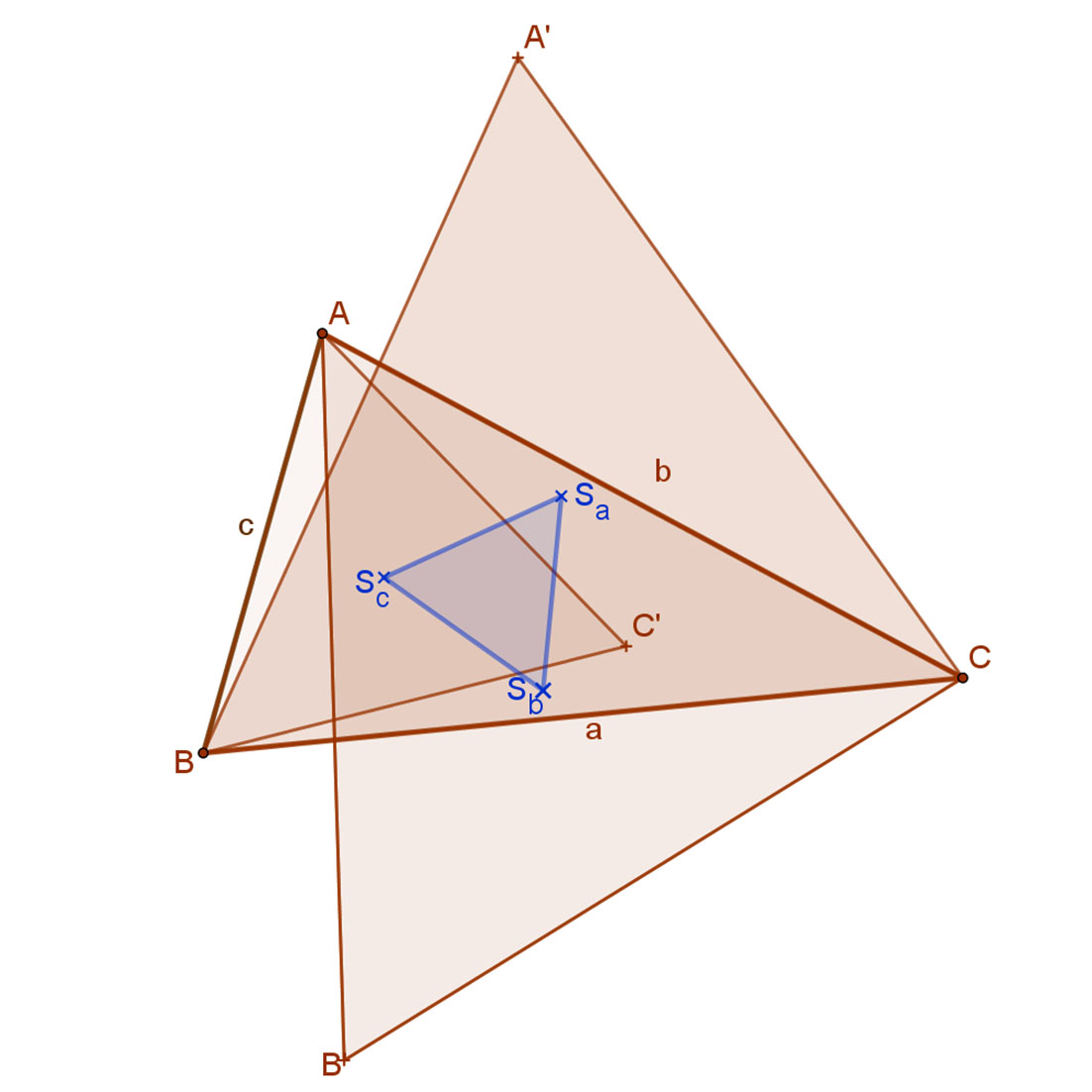
Tétel:

Ha az ABC nem egyenlő oldalú háromszög oldalaira befelé emelünk egy-egy szabályos háromszöget, akkor ezen szabályos háromszögek középpontjai mindig szabályos háromszöget alkotnak. Ezt a szabályos háromszöget az eredeti háromszög belső Napóleon-háromszögének nevezzük.

Ha az ABC háromszög egyenlő oldalú, akkor az oldalaira befelé szerkesztett szabályos háromszögek középpontjai egy pontba esnek, ezért nem alkotnak háromszöget.

A külső és belső Napóleon háromszögek területeire vonatkozó tétel:

A háromszöghöz tartozó külső és belső Napóleon-háromszög területének különbsége egyenlő az eredeti háromszög területével.

Egyenlő oldalú ABC háromszög esetén a külső Napóleon-háromszöge egybevágó az eredeti ABC háromszöggel, azzal egyenlő területű, a belső Napóleon háromszög pedig egy ponttá fajult, vagyis területe 0, tehát az egyenlő oldalú háromszögre is érvényes a Napóleon háromszögek területére vonatkozó tétel.

Megjegyzés: A hagyomány Bonaparte Napóleont a híres francia hadvezért és császárt tartja az összefüggések felismerőjének, de ez nincs bizonyítva.

https://hu.wikipedia.org/wiki/Nap%C3%B3leon-t%C3%A9telek