A) Két függvény összege; különbsége, szorzata és hányadosa.
Definíció:
Az f(x) és g(x) függvények összegén; különbségén, szorzatán, hányadosan azt a c(x) függvényt értjük, amely minden x0∈ Df ∩ Dg esetén.
· c(x0)=f(x0)+g(x0.)
· c(x0)=f(x0)-g(x0).
· c(x0)=f(x0)∙g(x0).
· c(x0)=f(x0)/g(x0), g(x0)≠0.
Megjegyzés: Az eredmény függvény értelmezési tartománya a két függvény értelmezési tartományának a közös része (metszete).
Példa:
Az alábbi grafikonokon a következő két függvénnyel láthatók a fenti műveletek: f(x)=sin(x);g(x)=√x.
Függvények összeadása, kivonása:
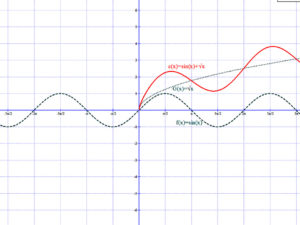
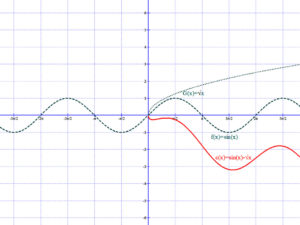
Függvények szorzata, hányadosa:
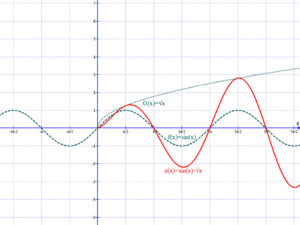
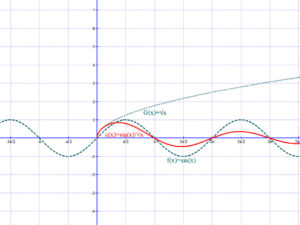
B) Összetett függvények
Definíció:
Az f: A→B és g: B → C függvények összetételén (kompozícióján) azt a h: A → C függvényt értjük, amelyre Dh={x∈ Df és f(x)∈ Dg}, továbbá h(x)=g(f(x)) teljesül minden x ∈ Dh esetén.
A h(x)=g(f(x)) esetén a g függvényt külső, az f függvényt belső függvénynek nevezzük.
Összetett függvények jelölése: h=g○f : h(x)=(g○f)=g(f(x))
Példa: Az alábbi grafikonokon a következő két függvénnyel láthatók példák függvények összetételére: l(x)=log2(x) és g(x)=√x,
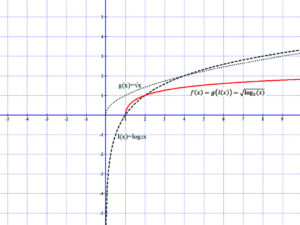
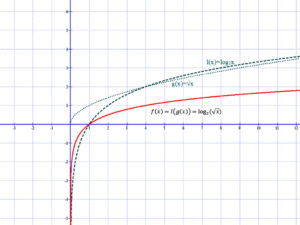


Comments are closed, but trackbacks and pingbacks are open.