Koszinusz tétel

Tétel:

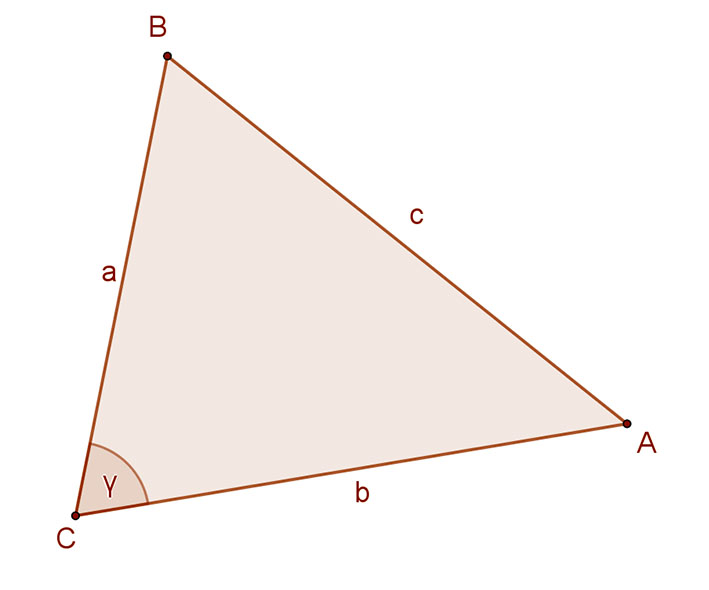
Bármely háromszögben az egyik oldal négyzetét megkapjuk, ha a másik két oldal négyzetének összegéből kivonjuk e két oldal és az általuk közbezárt szög koszinuszának kétszeres szorzatát.

Formulával: ​\( c^{2}=a^{2}+b^{2}-2·a·b·cosγ \)​.

Bizonyítás:

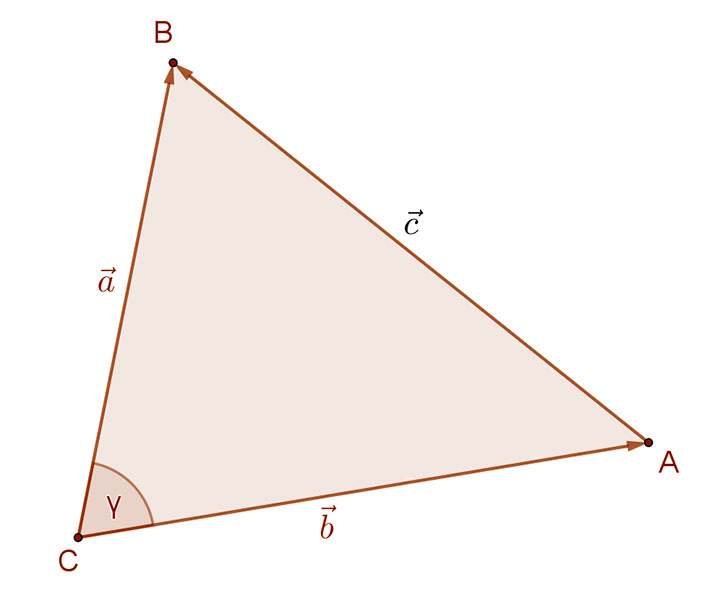Irányítsuk a háromszög oldalait az ábrán jelölt módon.
Az „a” oldal az ​\( \vec{a} \)​ vektor, „b” oldal a ​\( \vec{b} \)​ vektor és  a „c” oldal a ​\( \vec{c} \)​ vektor. Itt az ​\( \vec{a} \)​, a ​\( \vec{b} \)​ és a ​\( \vec{c} \)​ vektorok abszolút értéke a háromszög megfelelő oldalának hosszával egyenlő.
A ​\( \vec{c} \)​  vektor az ​\( \vec{a} \)​  és ​\( \vec{b} \)​ vektorok különbsége, azaz ​\( \vec{c} \)​= ​\( \vec{a} \)​-​\( \vec{b} \)​.
Emeljük négyzetre (​\( \vec{c} \)​  vektort szorozzuk önmagával skalárisan):
​\( \vec{c} \)²=(​\( \vec{a} \)​-​\( \vec{b} \))².

Felhasználva, hogy a skaláris szorzásnál is érvényes a disztributív tulajdonság: \( \vec{c} \)​²=\( \vec{a} \)​​²-2\( \vec{a} \)​\( \vec{b} \)​+\( \vec{b} \)​².

A skaláris szorzásnál definíciójából következik, hogy minden vektor önmagával vett skaláris szorzata egyenlő a vektor hosszának a négyzetével: \( \vec{c} \)​²=c², \( \vec{a} \)​²=a², \( \vec{b} \)​²=b².

Ugyancsak a skaláris szorzás definíciója szerint: \( \vec{a} \)​⋅\( \vec{b} \)​=abcosϒ.

Így kapjuk az állítást: c²=a²+b²-2⋅a⋅b⋅cosγ.

Természetesen a tétel és a bizonyítás a háromszög bármelyik oldalára igaz.

A koszinusz tételt felfoghatjuk a Pitagorasz tételének általánosításaként, amikor a háromszögnek a koszinusz tételben szereplő szöge éppen 90° . Ekkor cosγ =0 következtében a koszinusz tétel a Pitagorasz tételét adja: c²=a²+b².

A koszinusz tétel jól alkalmazható a háromszög adatainak meghatározásában:

1. Ha ismerjük a háromszög bármely két oldalát és a közbezárt szögét, a koszinusz tétel segítségével kiszámíthatjuk a háromszög harmadik oldalát.

2. Ha ismerjük a háromszög mindhárom oldalát, akkor a koszinusz tétel segítségével kiszámíthatjuk bármelyik szögét.

A koszinusz tételt szokás Carnot-tételnek is nevezni, a XVIII. századi francia matematikus után.