Körcikk és a körszelet területe

Meghatározások: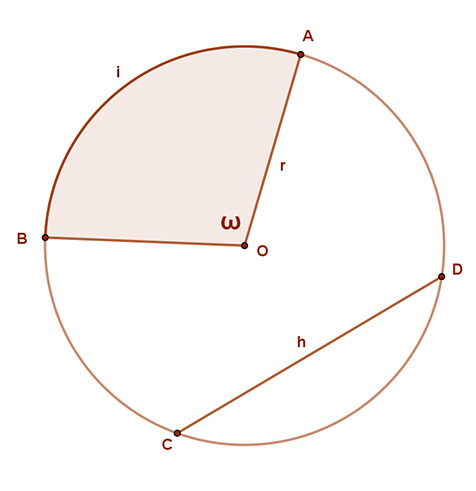

A körben a középponti szög csúcsa a kör középpontja, két szára a kör két sugara, illetve azok félegyenese. Egy középponti szög (ω) a körvonalból egy körívet (AB ív), a körlapból egy körcikket (AOB) határoz meg.
A körszelet a körlapnak a kör egy húrja (h) és a hozzátartozó körív (CD ív) által határolt része.

1. Körcikk területe.

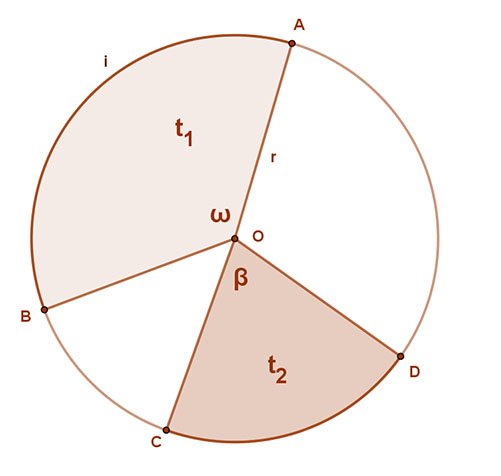Egy körben a középponti szög és a hozzátartozó körcikk területe egyenesen arányos.

Azaz kisebb középponti szöghöz kisebb területű, nagyobb középponti szöghöz nagyobb területű körcikk tartozik.

Ennek alapján felírhatjuk azt az arányt, amely egy adott körcikket meghatározó középponti szög és a teljes körhöz tartozó középponti szög, valamint a körcikk területe és a teljes kör területe között van: ​\( t_{körcikk}:t_{kör}=\hat{ω}:2 π \)​, ahol  ​\( \hat{ω} \)​ a középponti szög nagysága ívmértékben kifejezve.

Ugyanez az arány így írható, ha a középponti szöget fokban adjuk meg: ​\( t_{körcikk}:t_{kör}=ω:360° \)​ .

A kör területére vonatkozó képletet felhasználva:
​\( t_{körcikk}:r^{2} π =\hat{ω}:2 π \)​ (radiánban) illetve  ​\( t_{körcikk}:r^{2} π =ω:360° \)​ (fokban).
Szorzatalakba írva: ​
​\( t_{körcikk}·2 π =r^{2} π ·\hat{ω} \)​ , illetve ​\( t_{körcikk}·360° =r^{2} π ·ω \)​.

Átrendezve, π -vel egyszerűsítve kapjuk a körcikk területét:

​\( t_{körcikk}=\frac{r^{2} ·\hat{ω}}{2} \)​, illetve ​\( t_{körcikk}=\frac{ω}{360°}r^{2} π \)​.

Az ívmérték definíciója szerint: ​\( \hat{ω}=\frac{i}{r} \)​ . Ezt felhasználva:  ​\( t_{körcikk}=\frac{i·r}{2} \)​.

Megjegyzés:
A kapott  ​\( t_{körcikk}=\frac{i·r}{2} \) képlet nagyban hasonlít a háromszög területének jól ismert ​\( t_{△}=\frac{a·m_{a}}{2} \)​ képletéhez.

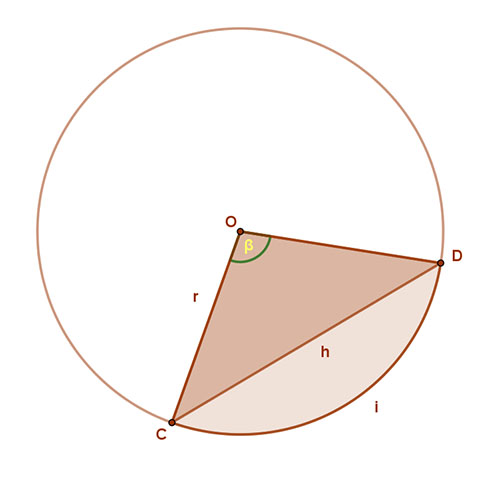2. Körszelet területe.

A körszelet területét úgy határozhatjuk meg, hogy a körcikk területéből kivonjuk a sugarak és húr által határolt háromszög területét.
A körcikk területe β középponti szög esetén:  ​\( t_{körcikk}=\frac{i·r}{2} \) , illetve ​\( t_{körcikk}=\frac{r^{2}·\hat{β}}{2} \)​.

A háromszög területe a két oldal és közbezárt szög területével: ​\( t_{△}=\frac{r^{2}·sinβ}{2} \)​ .

A körszelet területe tehát: ​\( t_{körszelet}=\frac{i·r}{2}-\frac{r^{2}·sinβ}{2}=\frac{r}{2}\left(i-r·sinβ \right) \)​

Másképp: ​\( t_{körszelet}=\frac{r^{2}·\hat{β}}{2}-\frac{r^{2}·sinβ}{2}=\frac{r^{2}}{2}\left(\hat{β}-sinβ \right) \)​.