Mit is jelent ez?
Már az ókori matematikusokat (Például Arkhimédész, Hippokratész, Eratoszthenész) izgatta az a kérdés, hogyan lehet egy adott kör területével egyenlő területű négyszöget szerkeszteni.
|
|
= ?
|
|
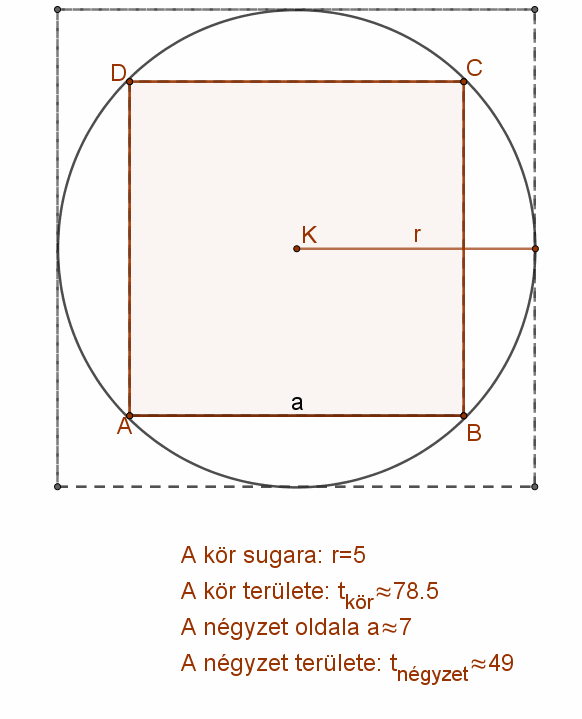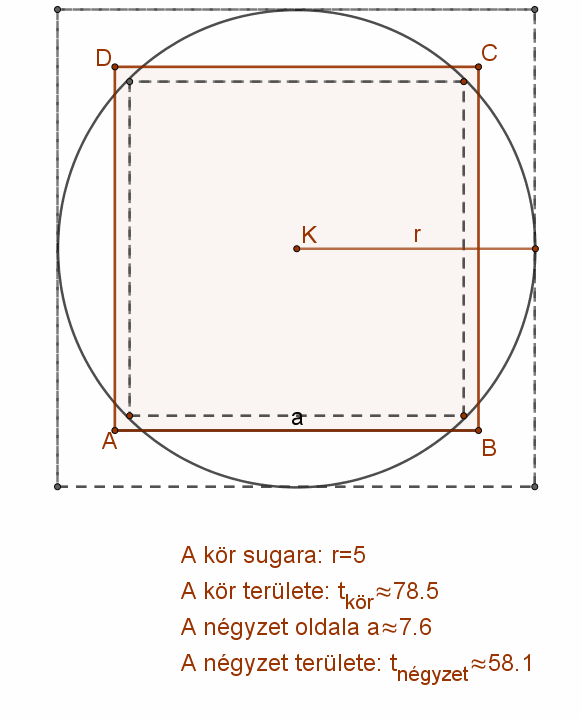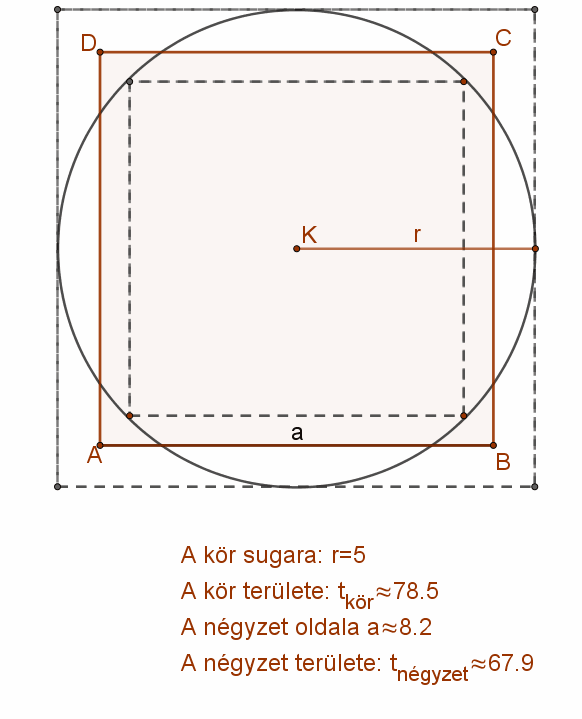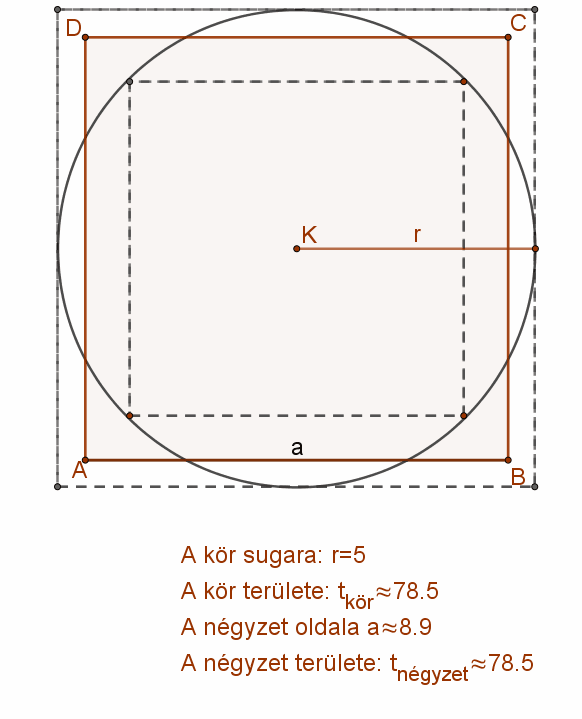 Az, hogy egy adott körrel egyező területű négyzetnek lennie kell, elég könnyen belátható. Szerkesszünk az adott r sugarú körbe beírt és köréírt négyzetet. A beleírt négyzet területe kisebb, a köréírt négyzet területe pedig nagyobb, mint a kör területe.
Az, hogy egy adott körrel egyező területű négyzetnek lennie kell, elég könnyen belátható. Szerkesszünk az adott r sugarú körbe beírt és köréírt négyzetet. A beleírt négyzet területe kisebb, a köréírt négyzet területe pedig nagyobb, mint a kör területe.
Azaz: \( b^{2}<t_{kör}<k^{2} \)
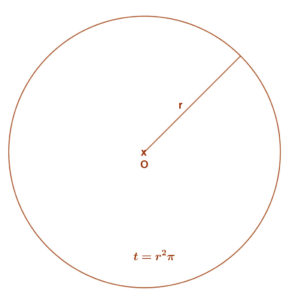
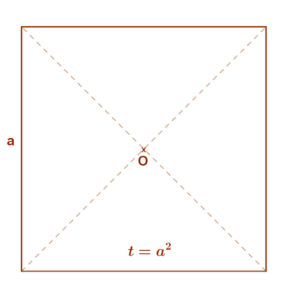
A beírt négyzet oldalát folyamatosan növelve, vagy a köré írt oldalát csökkentve kell legyen egy olyan állapot, amikor a négyzet területe éppen a kör területével egyezik meg. \( a^{2}=t_{kör}=r^{2} π \)
Nézzük a fenti egyenletet: a2 =r2⋅π. Ebből négyzetgyökvonás után kapjuk, hogy \( a=r·\sqrt{ π } \).
Ez pontosan azt jelenti, hogy adott szakasz (egység) esetén a π négyzetgyökét kellene megszerkeszteni. Persze a π szerkesztése is elegendő lenne, hiszen a negyedik arányos segítségével a négyzetgyökét is elő tudnánk állítani.
Ma már tudjuk (a XIX. század végétől), hogy euklideszi módon a π nem szerkeszthető, tehát nem szerkeszthető ilyen módon olyan négyzet, négyszög sem, amelynek a területe egy adott kör területével lenne egyenlő.
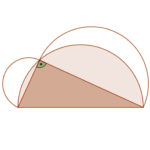 Hippokratész holdjai nagyszerű példája annak, hogy lehetséges egy adott sokszöggel (itt a derékszögű háromszöggel) egyenlő területű, de görbe vonalakkal határolt síkidomot szerkeszteni. Itt a két hold területének az összege éppen a háromszög területével egyenlő.
Hippokratész holdjai nagyszerű példája annak, hogy lehetséges egy adott sokszöggel (itt a derékszögű háromszöggel) egyenlő területű, de görbe vonalakkal határolt síkidomot szerkeszteni. Itt a két hold területének az összege éppen a háromszög területével egyenlő.
Bár euklideszi módon nem lehet a kör négyszögesítését megoldani, több jó közelítő szerkesztési eljárás is született a π szerkesztésére.


Comments are closed, but trackbacks and pingbacks are open.