Legyen adott két kör: Az O1 középpontú r1 sugarú (O1;r1) és az O2 középpontú r2 sugarú kör (O2;r2).
Két kör lehetséges kölcsönös helyzetét az alábbi animáció szemlélteti:
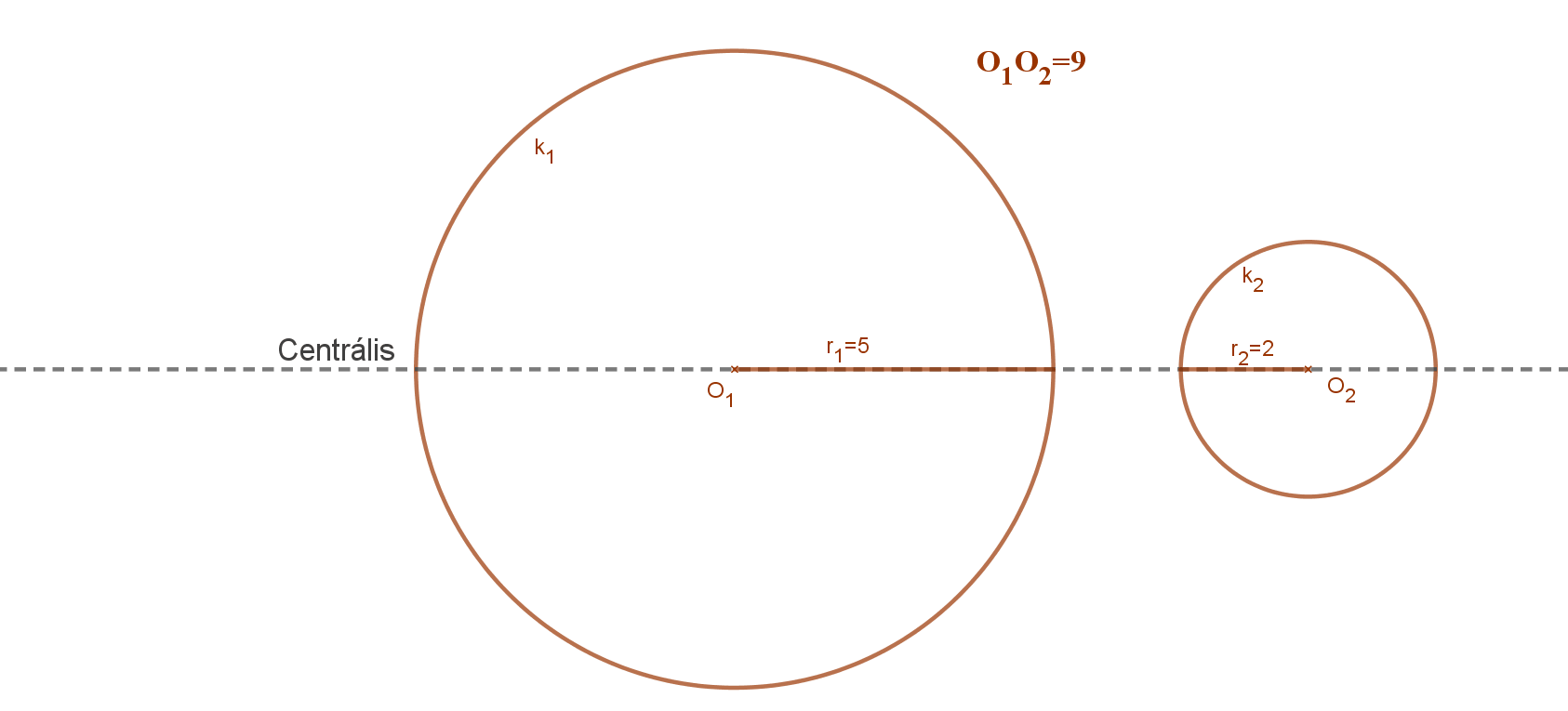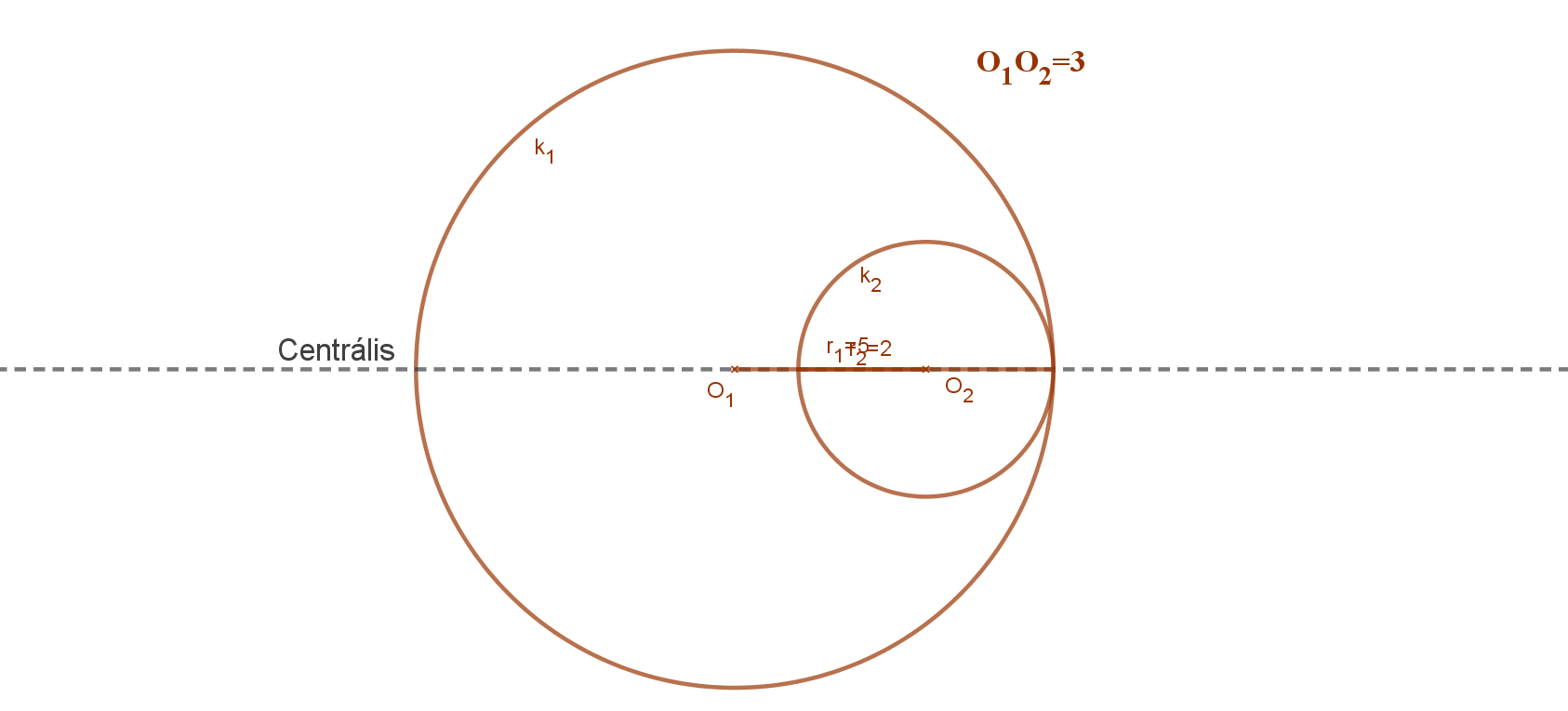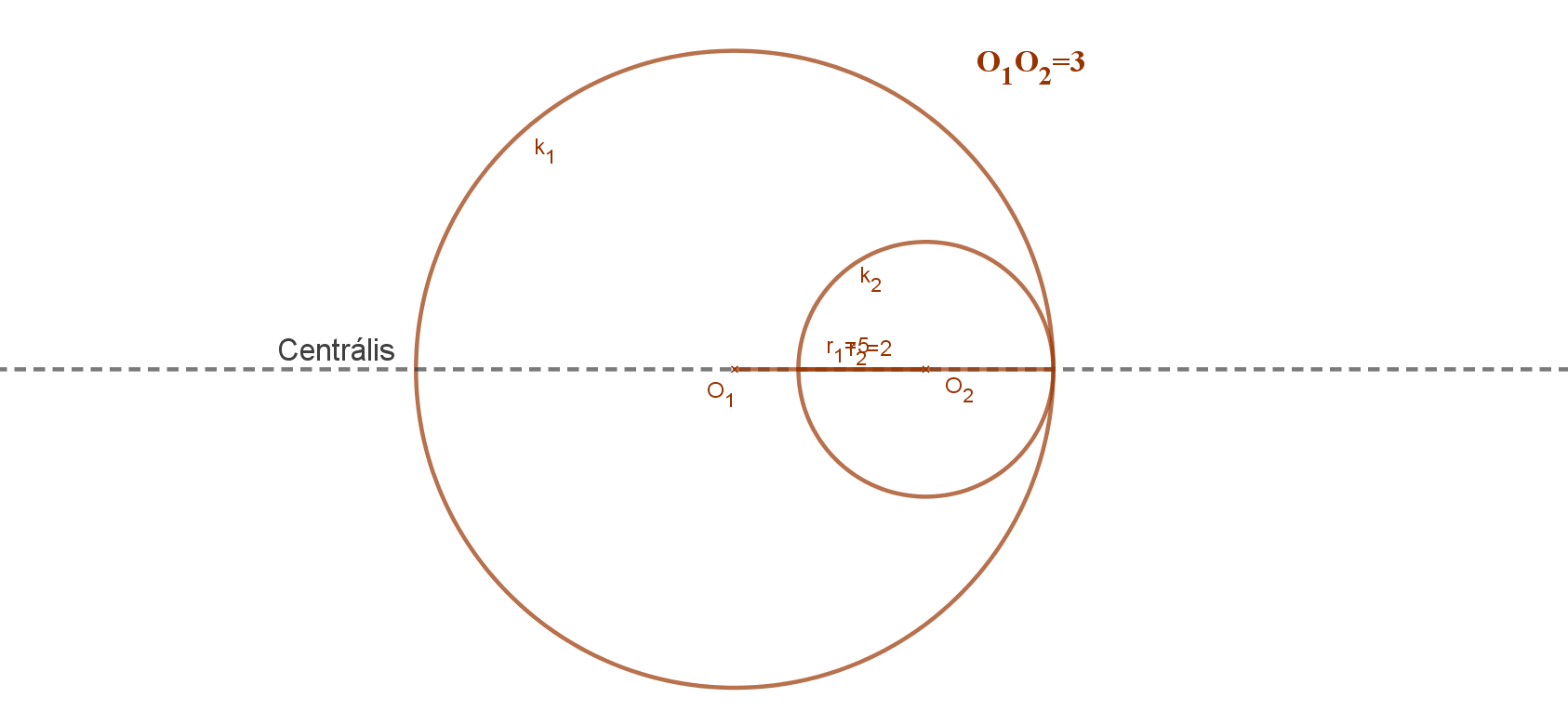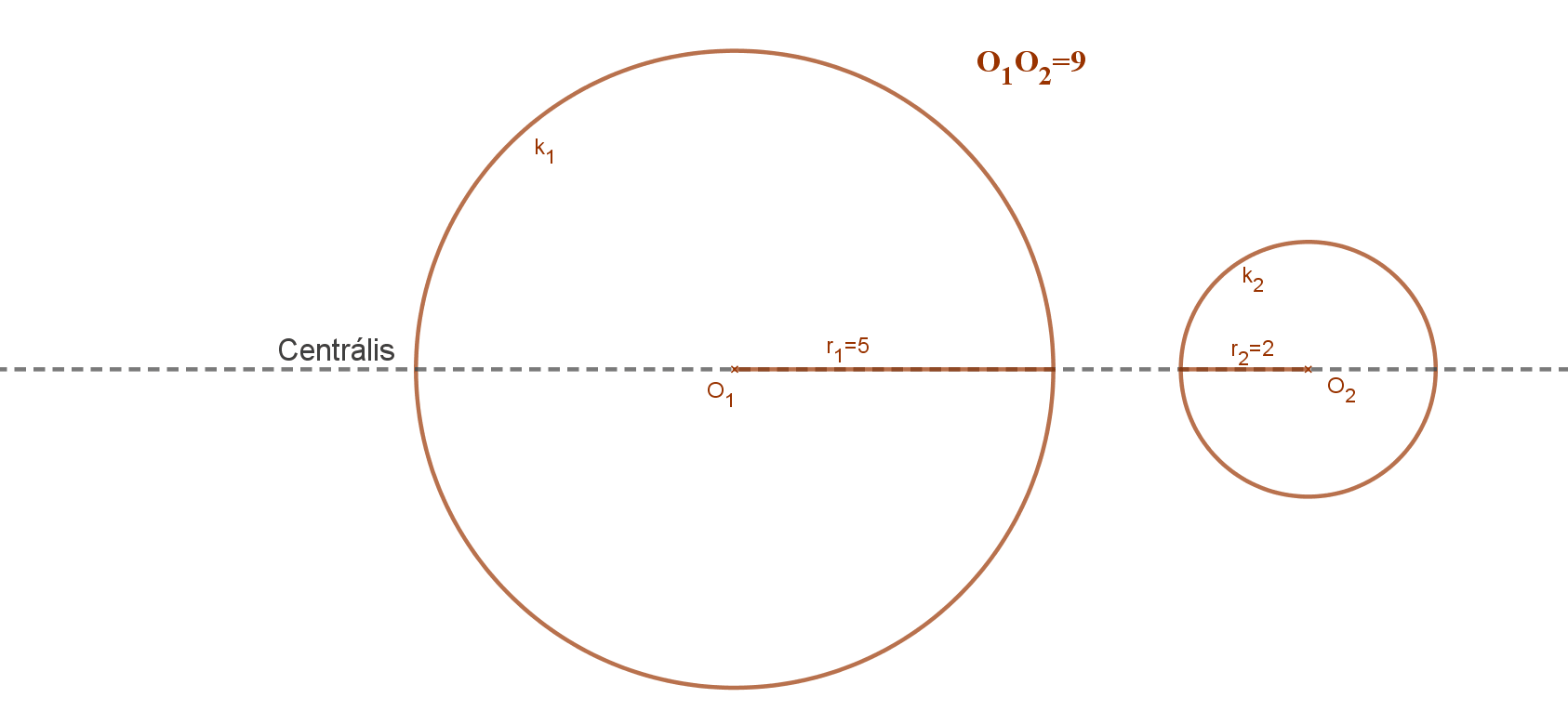
Hat különböző esetet figyelhetünk meg: O1O2>r1+r2.
1. A két körnek (körlemeznek) nincs közös pontja. O1O2>r1+r2.
2. A két kör kívülről érinti egymást. O1O2=r1+r2.
3. A két kör metszi egymást. |r1-r2|<O1O2<r1+r2.
4. A két különböző sugarú kör belülről érinti egymást. O1O2=|r1-r2|≠0.
5. Az egyik kör tartalmazza a másik kör összes pontját, de két kör középpontja nem esik egybe. 0<O1O2<|r1-r2|≠0.
6. Az egyik kör tartalmazza a másik kör összes pontját és a két kör középpontja egybe esik. 0=O1O2<|r1-r2|≠0.
Következőkben részletesebben megmutatjuk az egyes eseteket, feltüntetve a lehetséges közös érintőket is.
A közös érintők szerkesztését lásd itt.
1. eset. A két körnek (körlemeznek) nincs közös pontja.
Ekkor a két középpont távolsága nagyobb, mint a két kör sugara hosszának összege. O1O2>r1+r2.
 |
 |
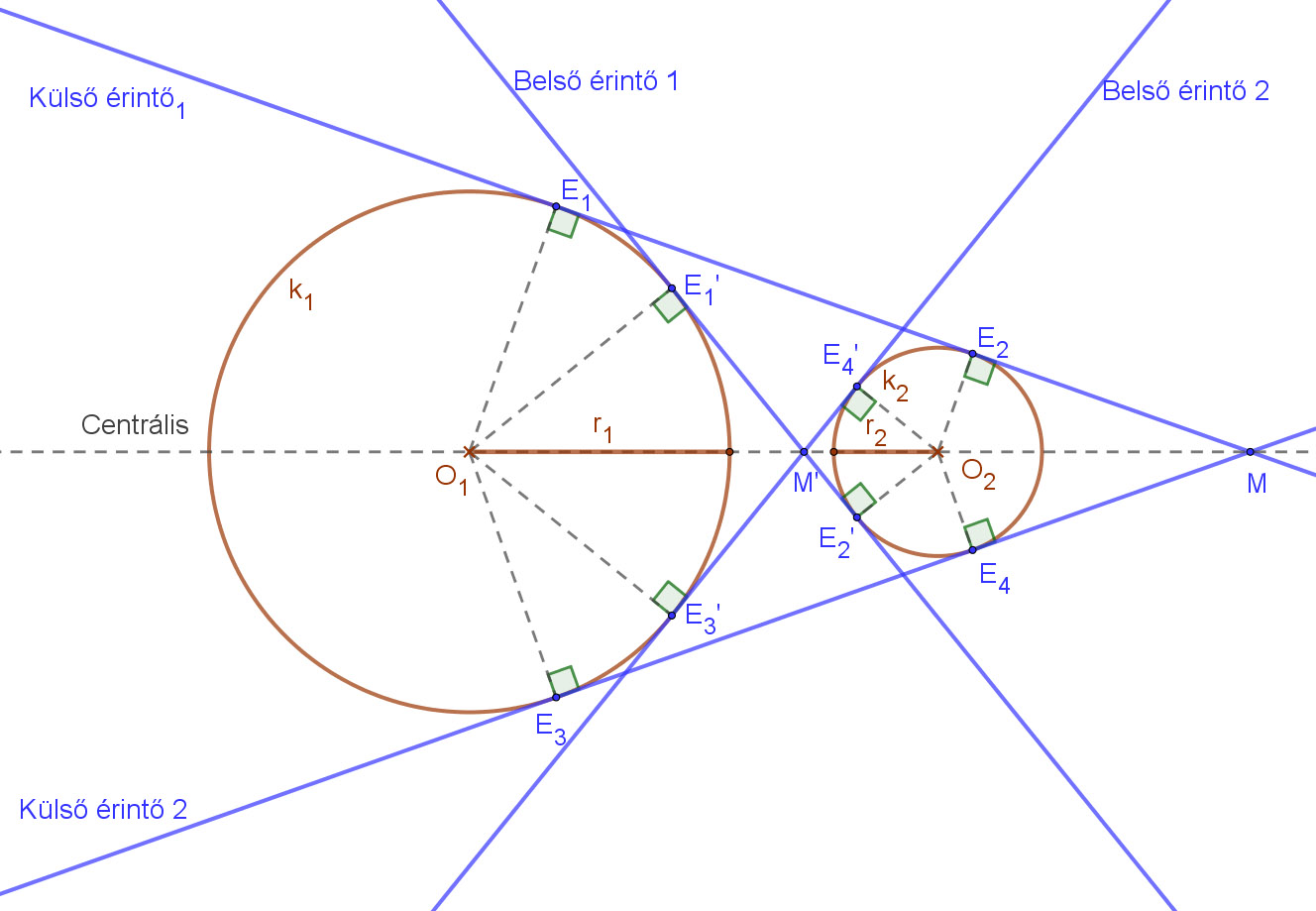
| Ha a két kör sugara különböző hosszúságú (r1 ≠ r2), akkor a köröknek két külső és két belső közös érintője van. A külső érintők a centrálison metszik egymást, az O1O2 szakaszon kívül. A belső érintők metszéspontja a centrálison az O1O2 szakasz belső pontja. |
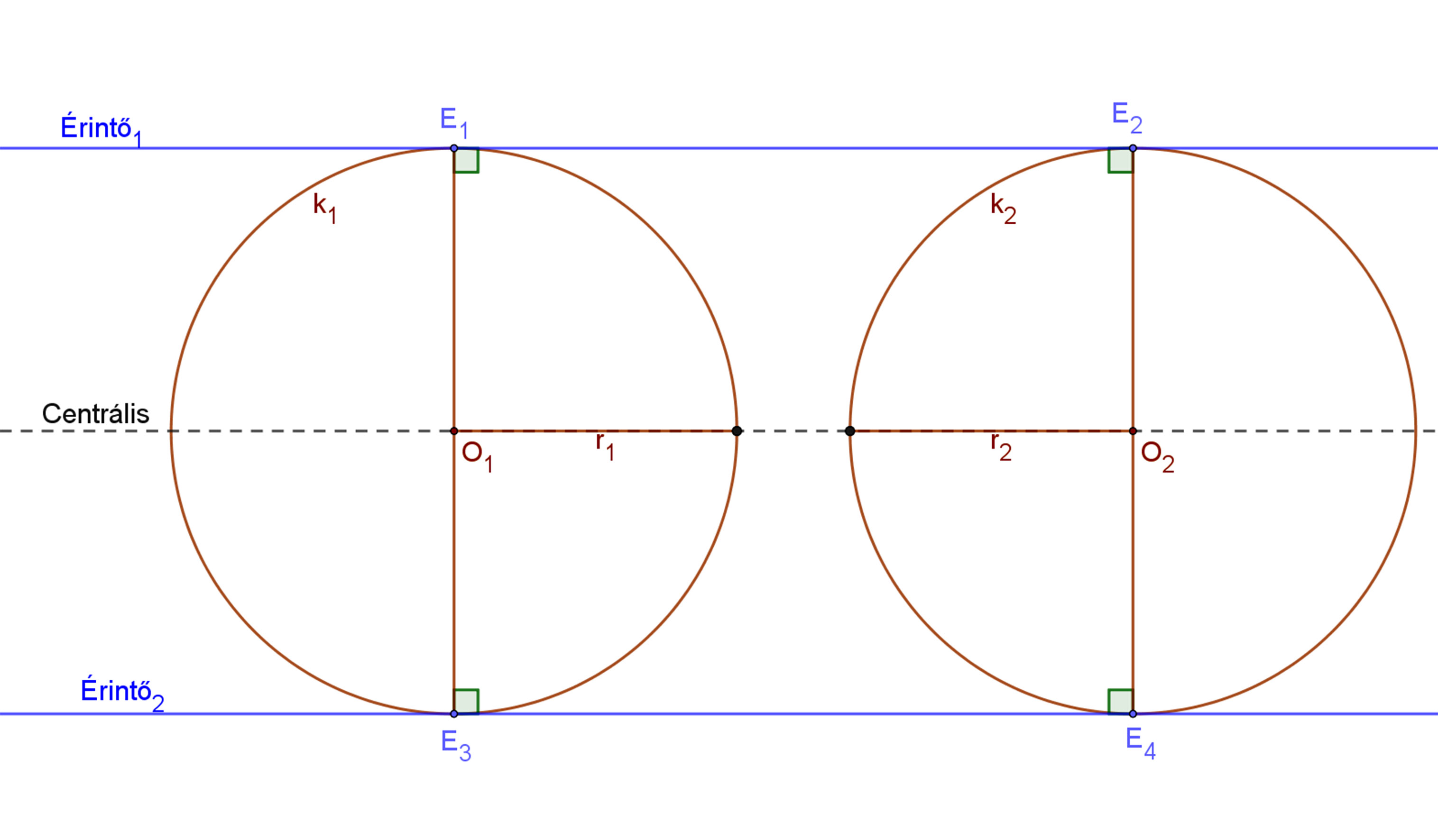
Ha a két kör sugara egyenlő hosszúságú (r1=r2), akkor a köröknek csak két közös érintője van. Ezek nem metszik egymást, hanem párhuzamosak az O1O2 pontok által meghatározott centrális egyenessel. |
2. eset: A két kör kívülről érinti egymást.
Ekkor a két középpont távolsága megegyezik a két kör sugara hosszának összegével. O1O2=r1+r2.
 |
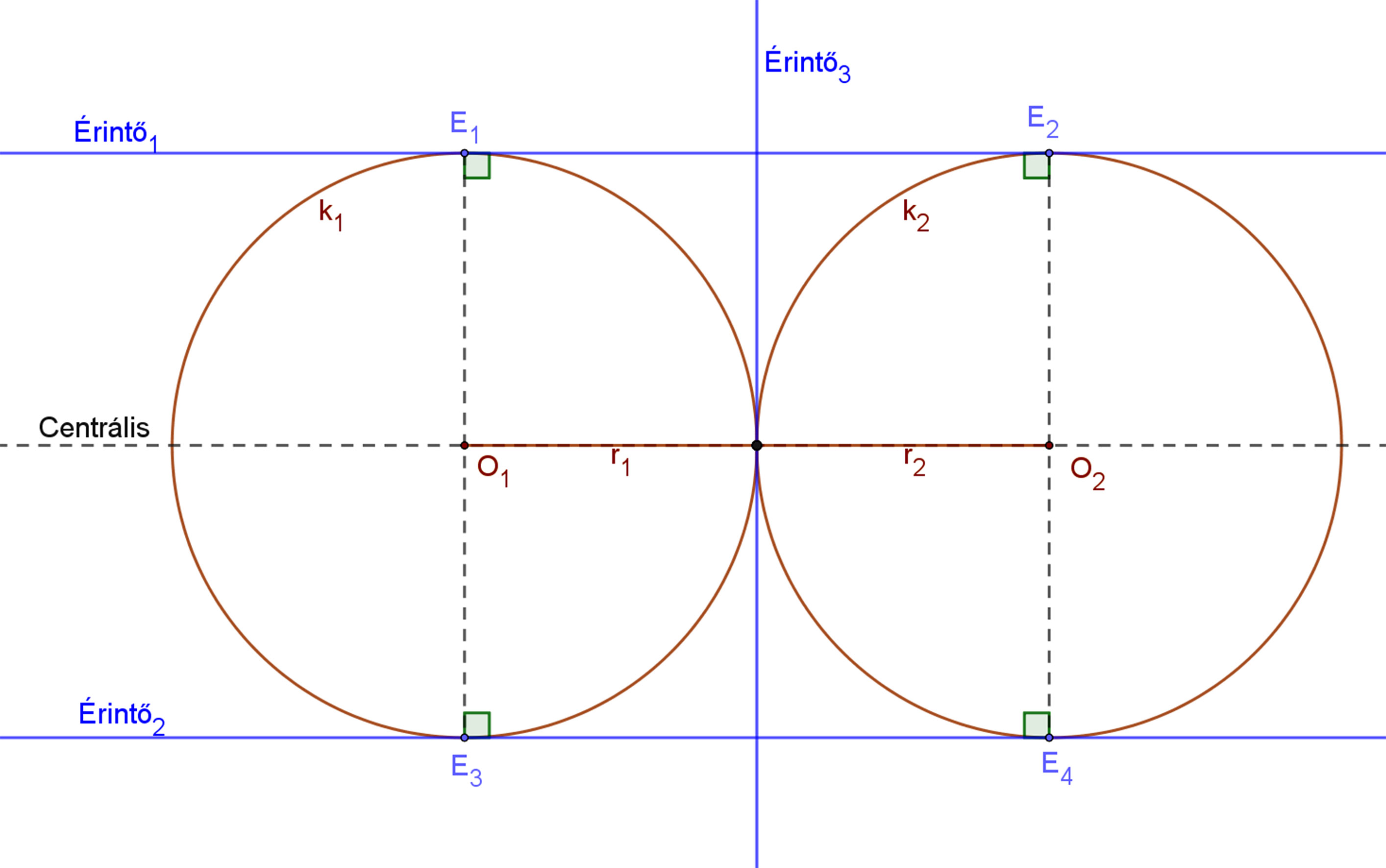 |
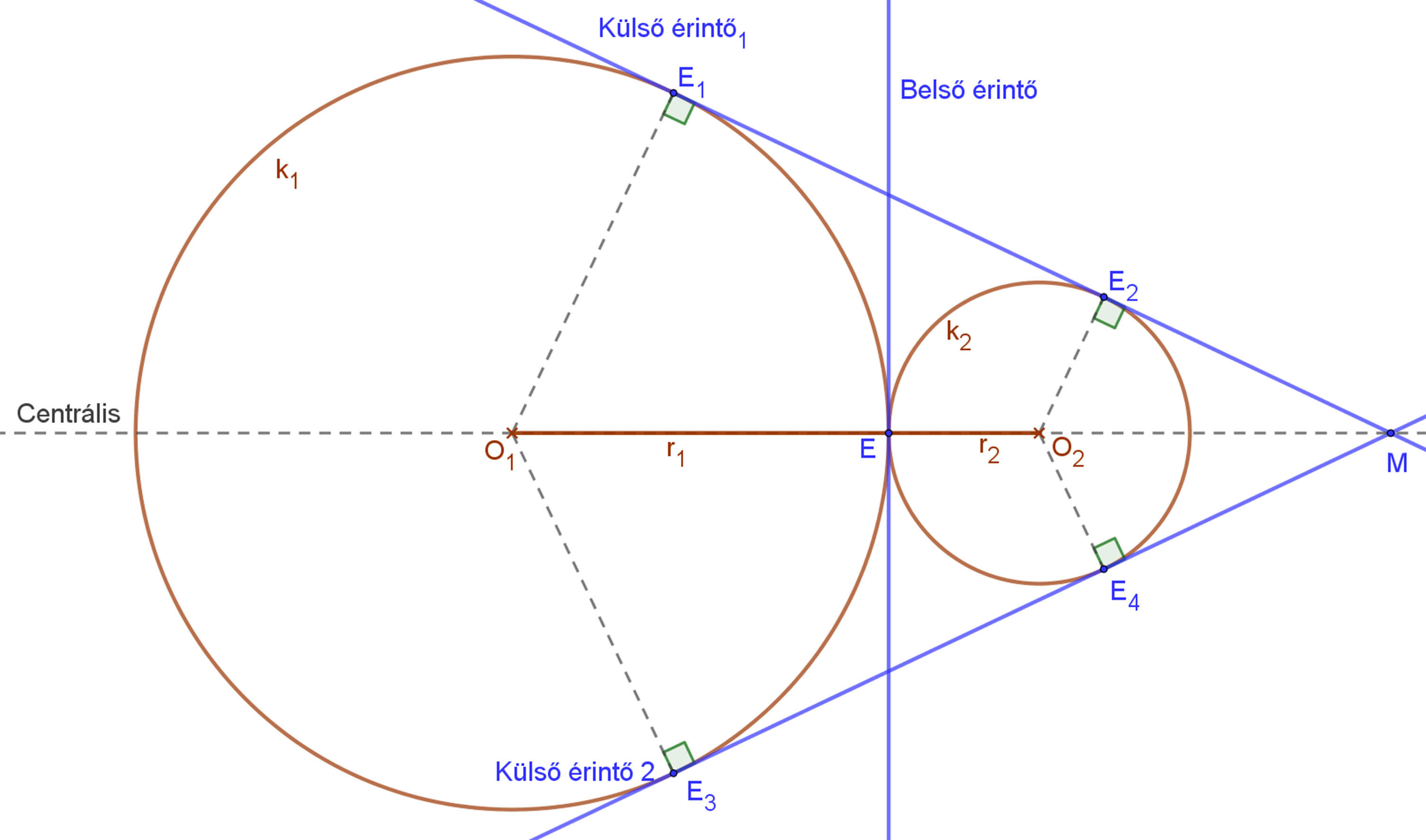
| Ha a két kör sugara különböző hosszúságú (r1≠r2), akkor a köröknek két külső és egy belső közös érintője van. A külső érintők a centrálison metszik egymást, az O1O2 szakaszon kívül. A belső érintő a két kör érintkezési pontjában merőleges a középpontokat összekötő centrális egyenesre. | Ha a két kör sugara egyenlő hosszúságú (r1=r2), akkor a köröknek két „külső” és egy belső közös érintője van. A két „külső” érintő párhuzamos a körök középpontjain áthaladó centrálissal. A harmadik érintő pedig a két kör érintkezési pontjában merőleges a középpontokat összekötő centrális egyenesre. |
3. eset: A két kör metszi egymást. |r1-r2|<O1O2<r1+r2.
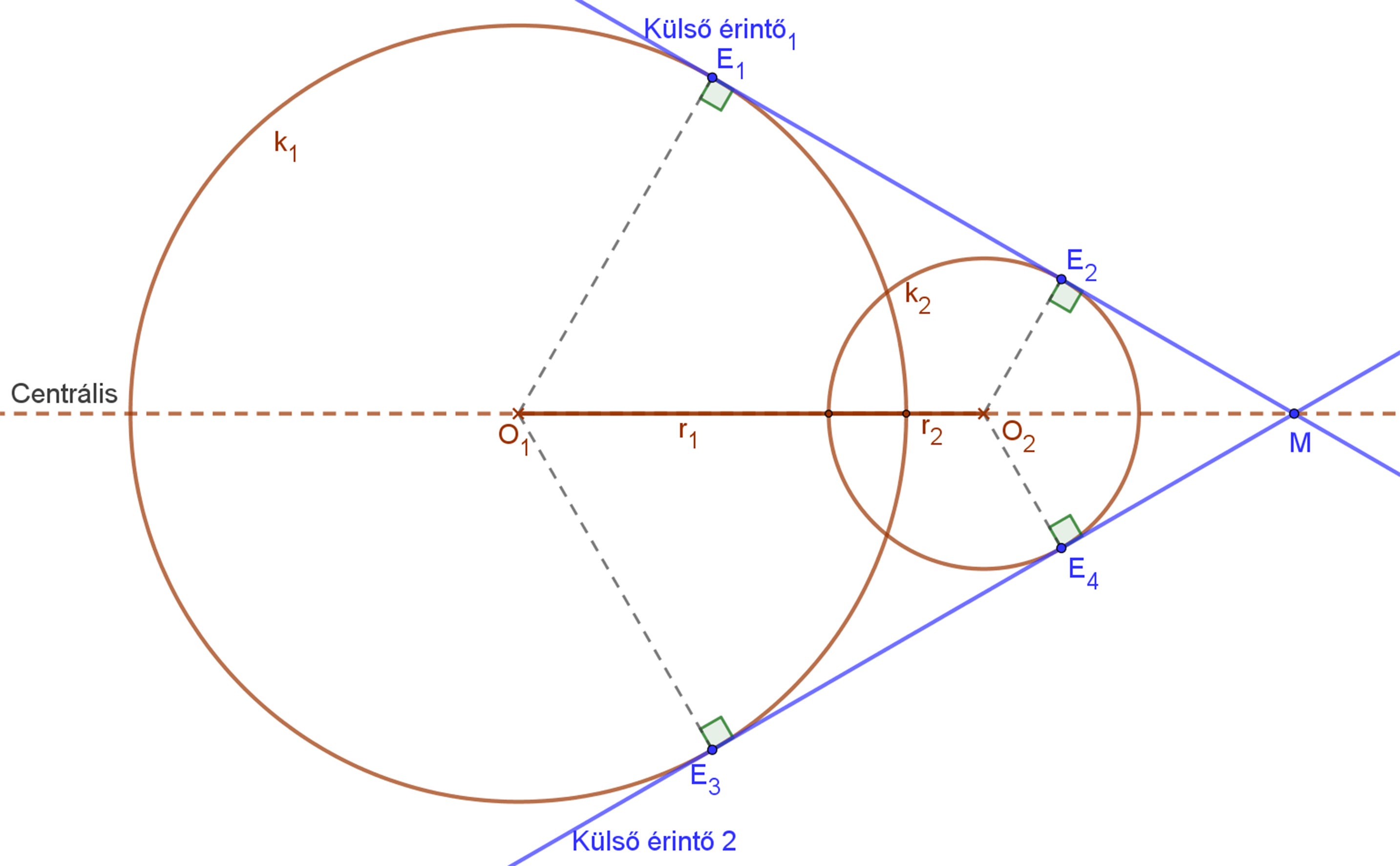 |
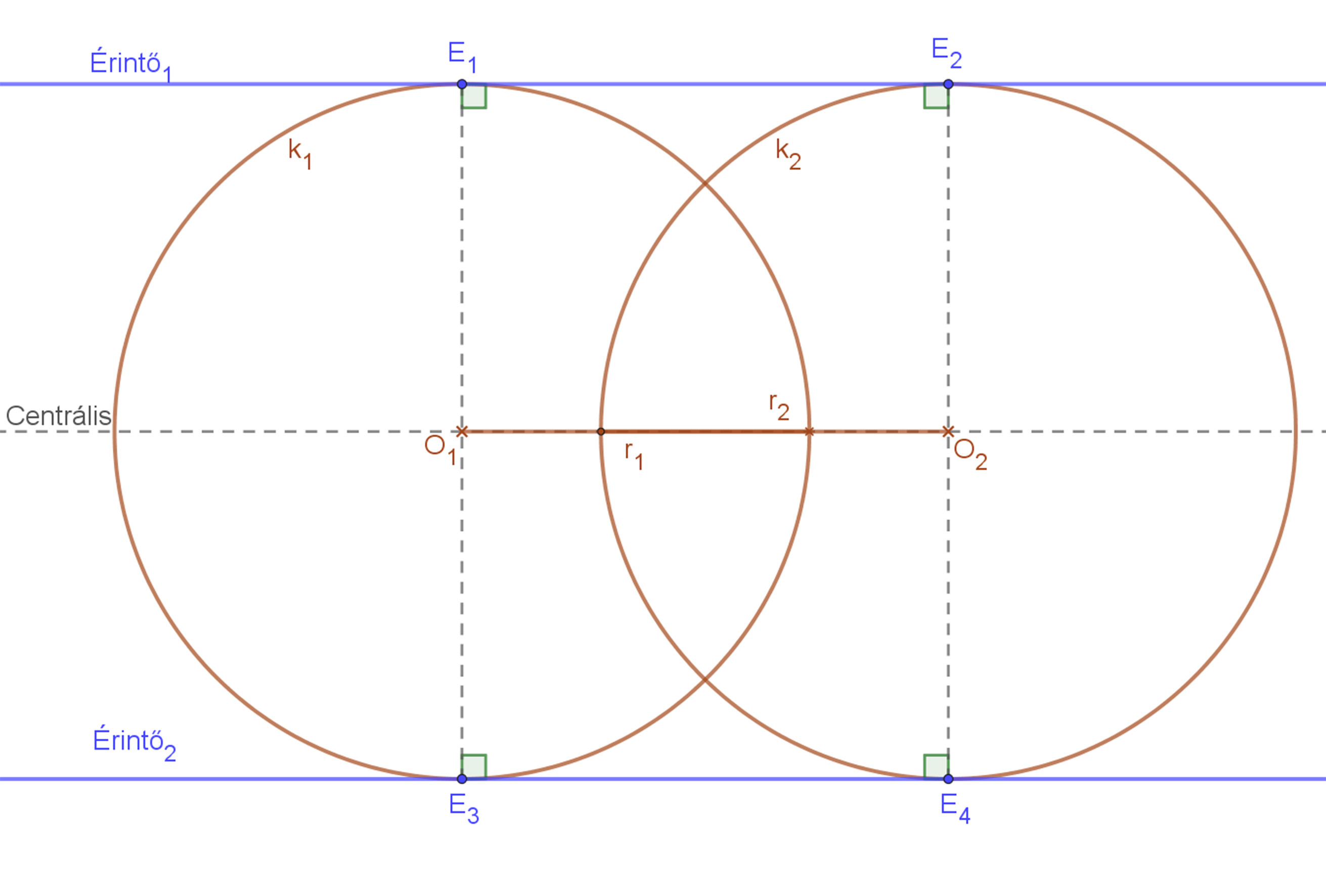 |
| Ebben az esetben, ha a két kör sugara különböző hosszúságú (r1≠r2), akkor a köröknek két külső közös érintője van. Ezek az érintők a centrálison metszik egymást, az O1O2 szakaszon kívül. |
Ha a két kör sugara egyenlő hosszúságú (r1=r2), akkor a köröknek csak két közös érintője van. A két érintő párhuzamos a körök középpontjain áthaladó centrálissal. |
4. eset: A két különböző sugarú kör belülről érinti egymást. O1O2=|r1-r2|≠0.
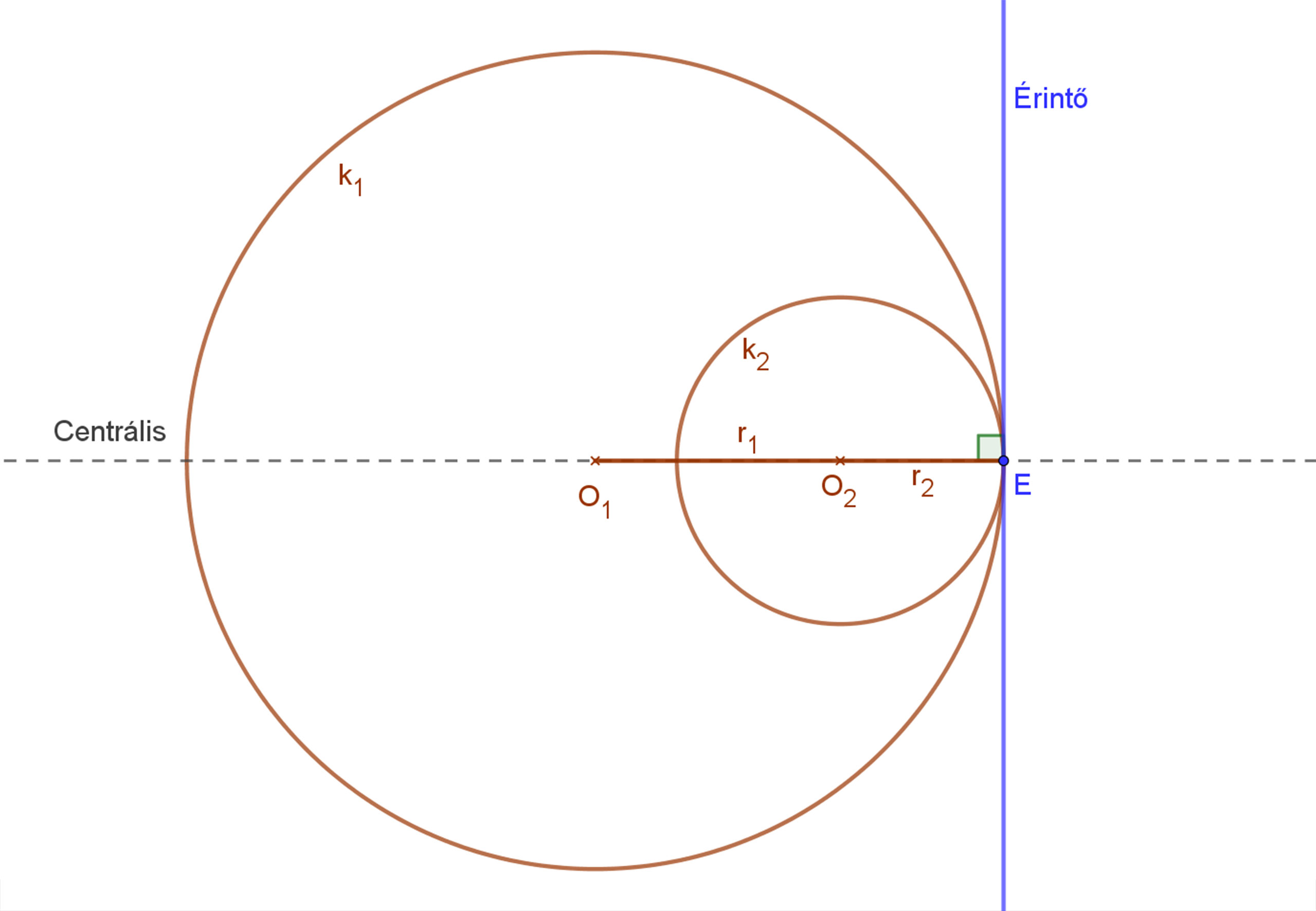
Ebben az esetben a két kör sugara nem lehet egyenlő ( r1≠r2), különben a két kör egybe esne, azaz fednék egymást.
A közös érintő a két kör érintési pontjában a centrálisra állított merőleges egyenes.
5. eset: Az egyik kör (körlemez) tartalmazza a másik kör összes pontját, de a két kör középpontja nem esik egybe.
0< O1O2 <|r1-r2|≠0.
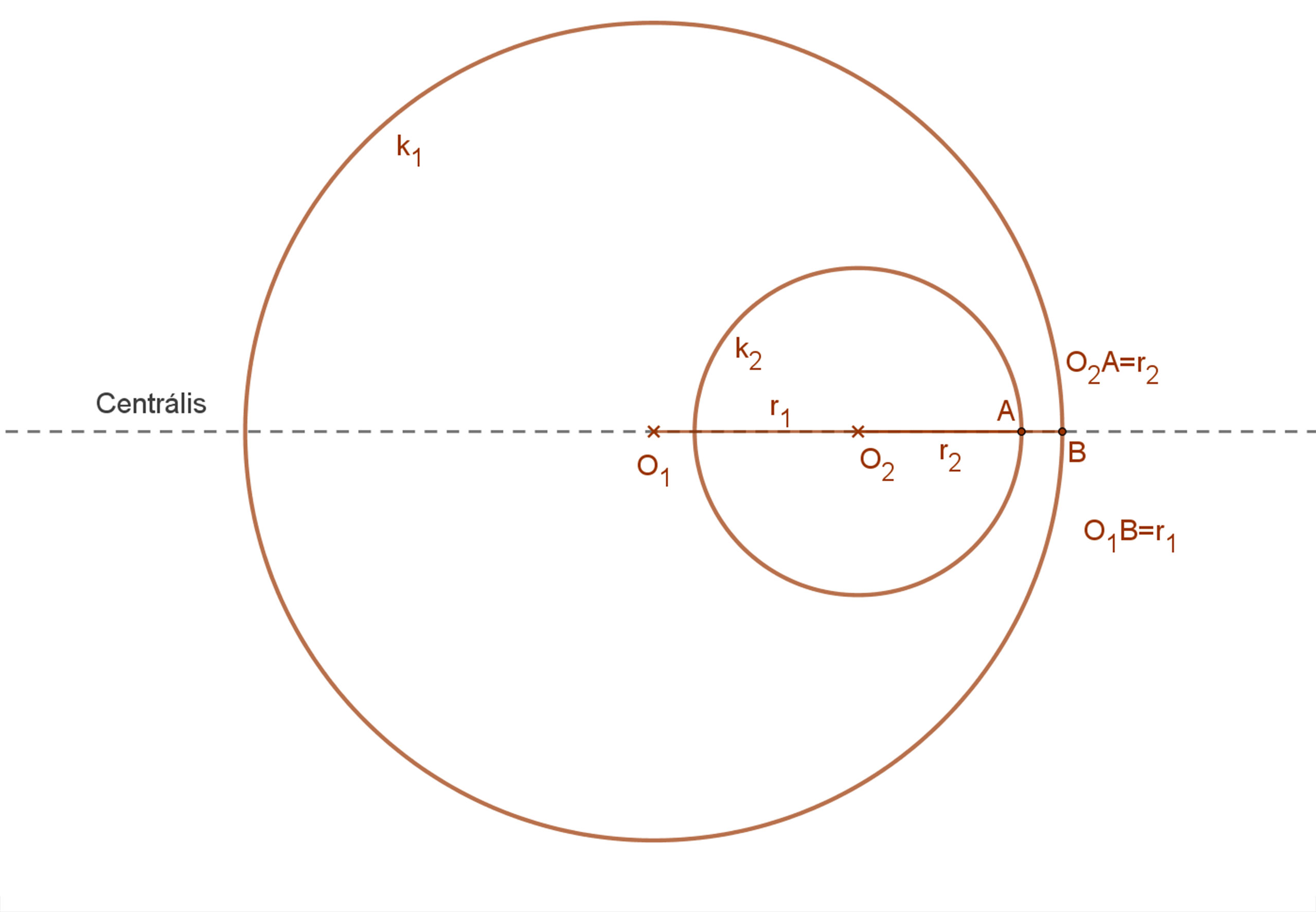
Ebben az esetben nem húzható olyan egyenes, amely mindkét kört érintené.
6. eset: Az egyik kör (körlemez) tartalmazza a másik kör összes pontját és a két kör középpontja egybe esik.
0=O1O2 <|r1-r2|≠0.

Ekkor koncentrikus körökről beszélünk.
Természetesen ebben az esetben sem húzható olyan egyenes, amely mindkét kört érintené.

