1. Feladat
Határozzuk meg az \( a_{n}=\frac{n^3+2n+1}{2n^3-n^2+3} \) sorozat határértékét!
Megoldás
Osszuk el a számlálót és a nevezőt is n3-nel.
Ekkor az algebrai tört számlálója \( 1+\frac{2}{n^2}+\frac{1}{n^3} \) lesz. Mivel \( \lim_{ n \to \infty }\frac{2}{n^2}=0 \; és \; \lim_{ n \to \infty }\frac{1}{n^3}=0 \), ezért \( \lim_{nx \to\infty}\left( 1+\frac{2}{n^2}+\frac{1}{n^3} \right) =1 \).
Az algebrai tört nevezője \( 2-\frac{1}{n}+\frac{3}{n^3} \) lesz. Mivel \( \lim_{ n \to \infty }\frac{1}{n}=0 \; és \; \lim_{ n \to \infty }\frac{3}{n^3}=0 \), ezért \( \lim_{ n \to \infty }\left(2-\frac{1}{n}+\frac{3}{n^3} \right) =2 \) .
Tehát: \( \lim_{ n \to \infty }\left( \frac{n^3+2n+1}{2n^3-n^2+3} \right) =\frac{1}{2} \).
Az alábbi animáció ezt mutatja:
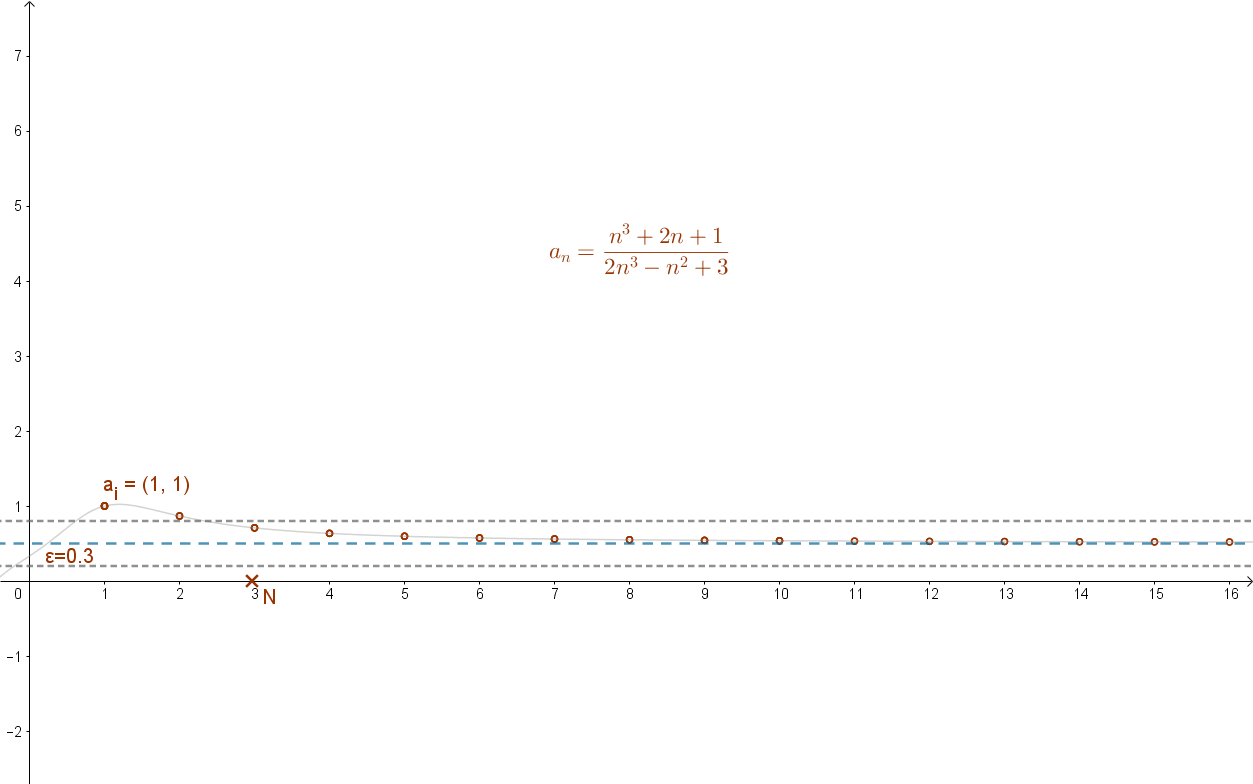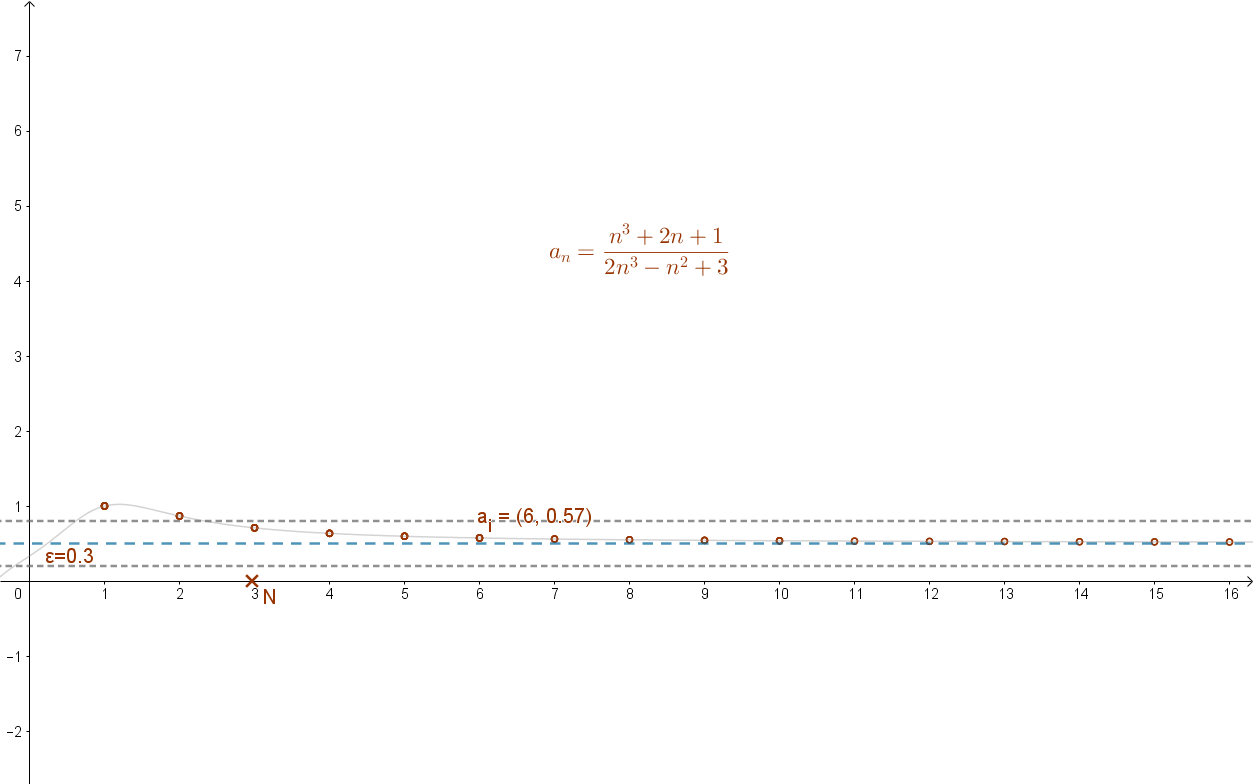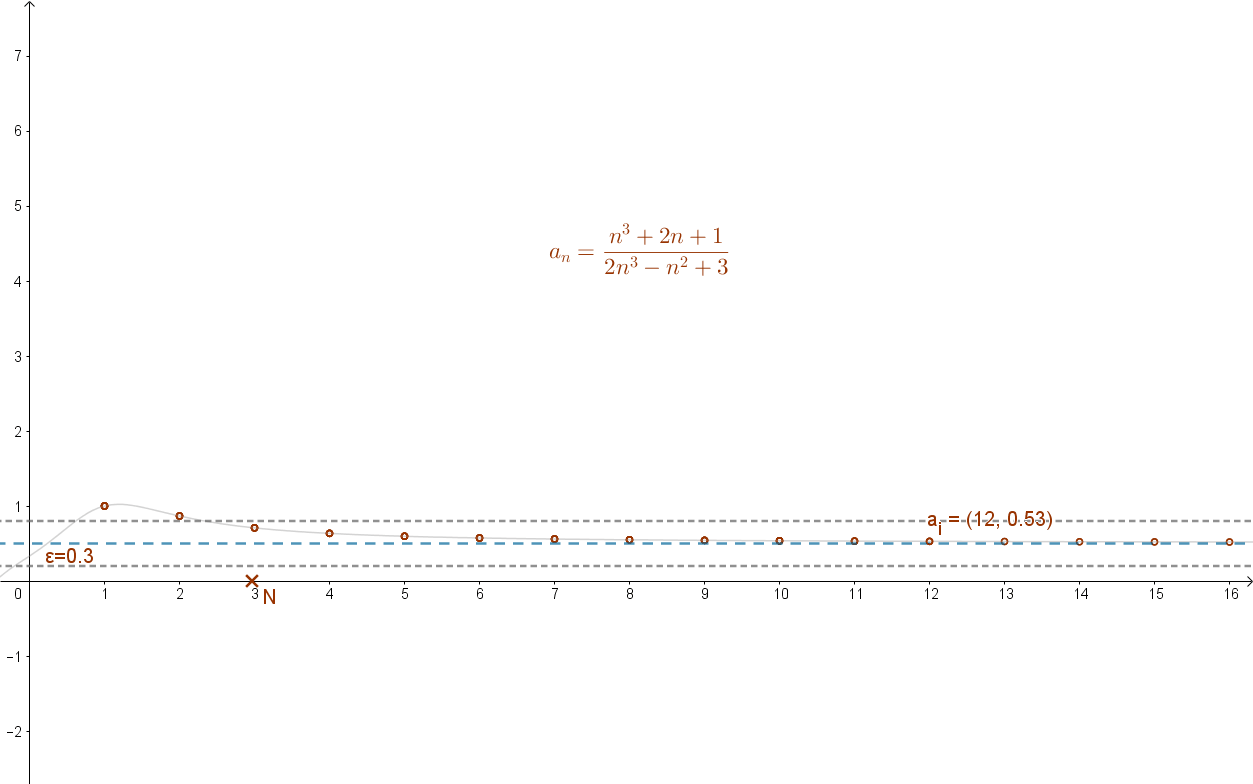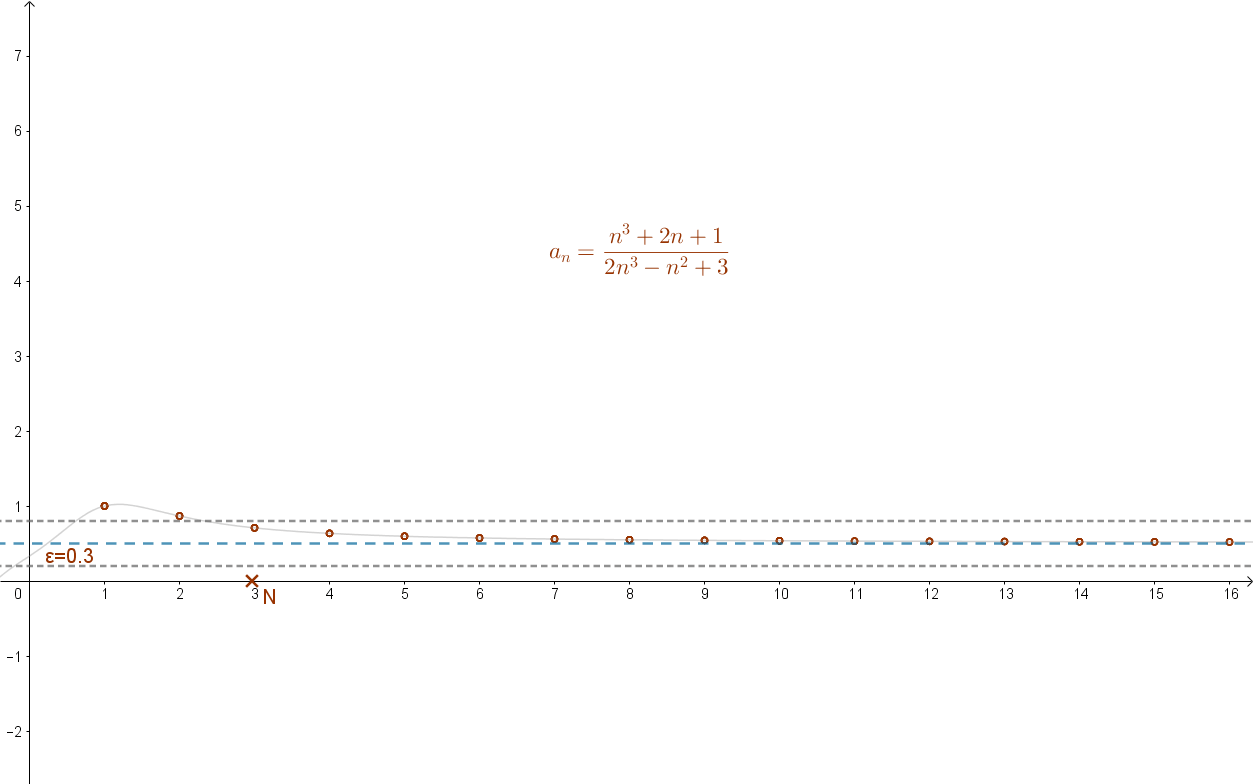
Általánosítva:
Ha egy sorozat két „n” –ben algebrai polinom hányadosa akkor a következő esetek lehetségesek:
• Ha a számláló és a nevező fokszáma azonos, akkor a sorozat konvergens és határértéke a legmagasabb fokszámú tagok együtthatóinak a hányadosa.
• Ha a nevező fokszáma nagyobb, mint a számláló fokszáma, akkor sorozat konvergens és határértéke = 0
• Ha a számláló fokszáma nagyobb, mint a nevezőé, akkor a sorozat divergens lesz és a + vagy – végtelenhez fog tartani.
2. Feladat
Határozzuk meg a következő sorozat határértékét \( d_{n}=\sqrt{n+1}-\sqrt{n-1} \) !
(NTK 14311/43. oldal)
Szorozzuk meg és osszuk el a sorozatot \( \sqrt{n+1}+\sqrt{n-1} \)-nel!
\( d_{n}=\frac{\left( \sqrt{n+1}-\sqrt{n-1} \right) ·\left(\sqrt{n+1}+\sqrt{n-1} \right) }{\left( \sqrt{n+1}+\sqrt{n-1} \right) } \).
Ekkor az (a2 –b2) azonosság alkalmazásával: \( d_{n}=\frac{(n+1)-(n-1)}{\sqrt{n+1}+\sqrt{n-1}}=\frac{2}{\sqrt{n+1}+\sqrt{n-1}} \).
Mivel itt a nevező a végtelenhez tart ( \( \lim_{n \to \infty }\sqrt{n+1}+\sqrt{n-1}=+∞ \) ) és a számláló konstans, ezért \( \lim_{ n \to \infty }= \frac{2}{\sqrt{n+1}+\sqrt{n-1}}=0 \).
3. Feladat
A „t” paraméter milyen értékei estén lesz konvergens az \( a_{n}=\left(\frac{t+4}{2t-3} \right)^n \) sorozat? (n=1; 2; 3;..;n;…).
(Összefoglaló feladatgyűjtemény Z/3659.)
Megoldás:
A feladat értelmezési tartománya: t≠1.5. (3/2), hiszen a nevező nem lehet nulla.
Egy {qn} sorozat csak akkor konvergens, ha -1<q≤1. Ekkor \( \lim_{ n \to \infty }q_{n} \)=0.
Ha -1<q<0 negatív, akkor a sorozat ugyan nem monoton (oszcilláló), de alulról és felülről is korlátos és határértéke nulla.
Ha 0<q≤1, akkor a sorozat szigorúan monoton csökken, alulról és felülről is korlátos. (k=0, K=q)
A feladat tehát a következő egyenlőtlenség-rendszer megoldását kívánja: \( -1<\frac{t+4}{2t-3}≤1 \).
A kifejezés, mint függvény egy lineáris törtfüggvény: \( f(t)=\frac{t+4}{2t-3}=\frac{1}{2}+\frac{5.5}{2(t-1.5)} \).
Az adott lineáris törtfüggvény szigorúan monoton csökkenő. Grafikonja hiperbola. Az y=1 egyenes az x=7. míg az y=-1 egyenes az x=-1/3 pontban metszik a görbét. A keresett megoldások a két párhuzamos által határolt sávban találhatók.
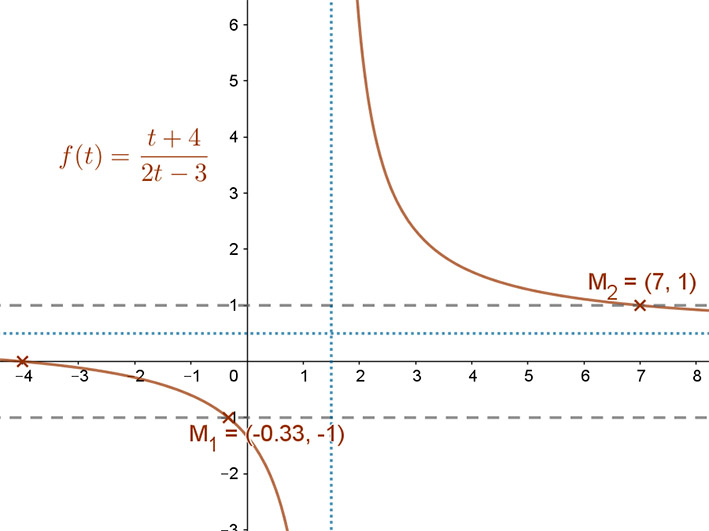
A monotonitásból következően az \( -1<\frac{t+4}{2t-3}≤1 \) egyenlőtlenség- rendszer eredményei: t1<-1/3, vagy t2≥7 .
Az \( a_{n}=\left(\frac{t+4}{2t-3} \right)^n \) sorozat tehát konvergens, ha t1<-1/3, vagy t2≥7 .
Megjegyzés: Ha t=-4, akkor a megadott sorozat konstans, hiszen a számlálója ekkor nulla.
Könnyen belátható, hogy t=7 esetén is konstans sorozatot kapunk, hiszen ekkor a számláló és a nevező is 11-gyel egyenlő. A konstans sorozat pedig konvergens.


Comments are closed, but trackbacks and pingbacks are open.