Hasonló síkidomok területe, hasonló gúlák térfogata

A) Hasonló sokszögek területe.

1. Hasonló sokszögek területeinek arányának vizsgálatát kezdjük a hasonló háromszögekkel.

Ha két háromszög hasonló, akkor egybevágósági transzformációk segítségével előállítható olyan helyzet, hogy a két háromszög középpontosan is hasonló, úgy hogy a hasonlóság aránya pozitív legyen.

Tekintsünk tehát két középpontosan hasonló háromszöget. Adottnak tekinthetjük a hasonlóság középpontját (O) és a hasonlóság arányát (λ>0).

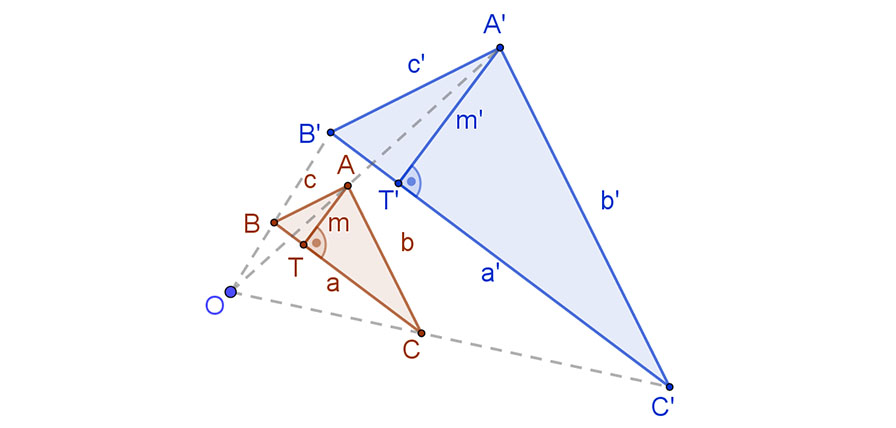Az O középpontú és λ arányú hasonlósági transzformáció az a oldalú m magasságú ABCΔ-ből a’=λ⋅a oldalú és m’=λ⋅m magasságú A’B’C’Δ -t hoz létre .

Az eredeti ABC háromszög területe: ​\( t_{ABC}=\frac{a·m}{2} \)​.

Az ABCΔ-höz hasonló A’B’C’Δ területe:  ​\( t_{A’B’C’}=\frac{λa·λm}{2}=\frac{λ^{2}a·m}{2}=λ^{2}·t_{ABC} \)​.

Azt kaptuk tehát, hogy a két háromszög területének aránya: t_A’B’C’ : t_ABC=λ².

2. Hasonló sokszögek területét vizsgálva, a sokszöget átlók segítségével háromszögekre bonthatjuk. Ebből következik, hogy bármely sokszög t területét a λ arányú hasonlósági transzformáció t’-re változtatja, úgy hogy hasonló sokszögek területeinek aránya a hasonlóság arányszámának a négyzetével egyenlő. t’:t=λ².

Megjegyzés: Bebizonyítható, hogy bármely hasonló síkidom (kör, ellipszis, stb.) területeinek aránya is: t’:t=λ².

B) Hasonló gúlák térfogata.

Tekintsünk két hasonló gúlát, amelyeknél a hasonlóság aránya λ.

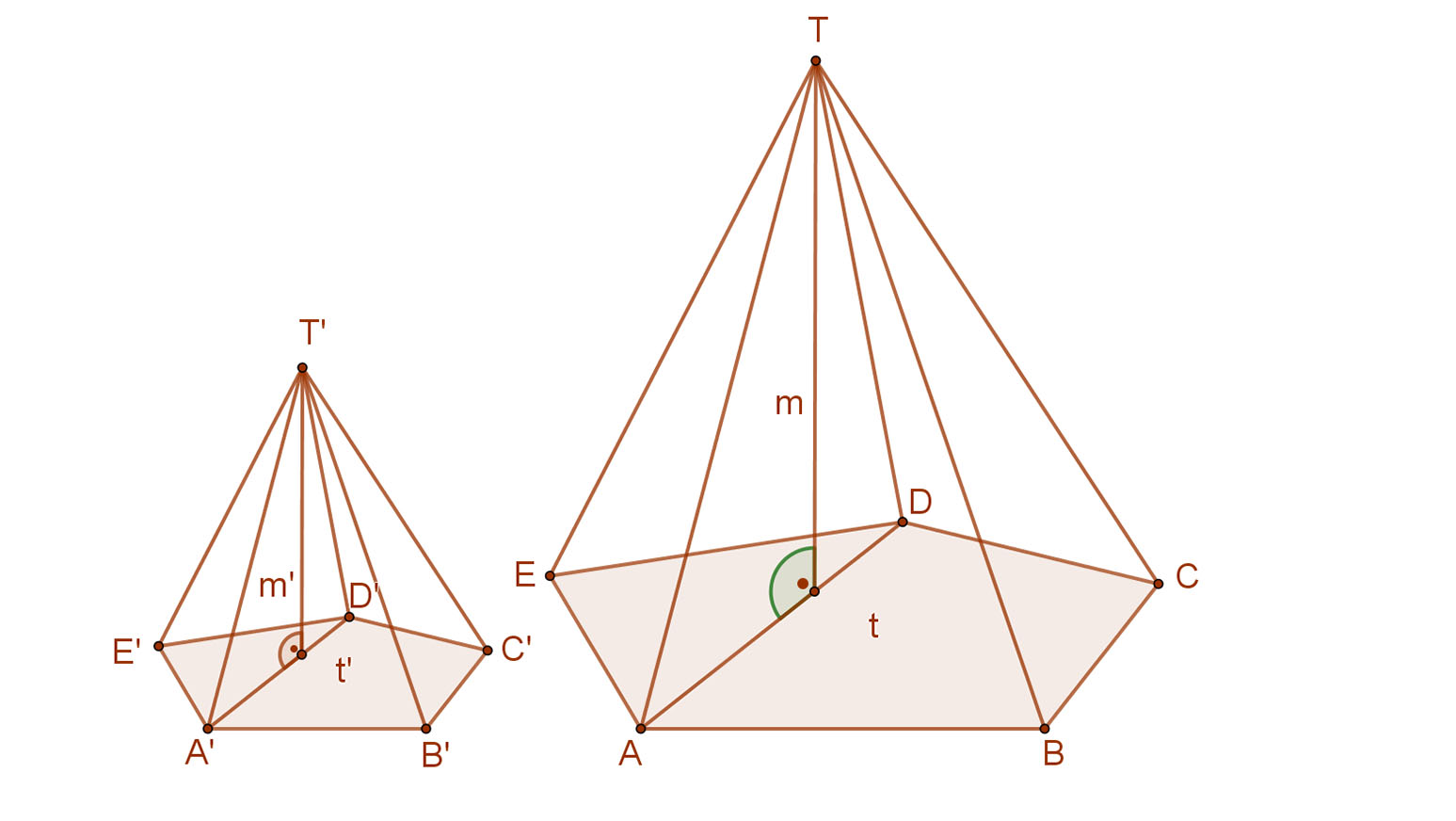
Az előzőekből következik, hogy az alaplapok területeinek aránya λ², azaz a mellékelt ábra betűzése szerint: t_{‘A’B’C’D’E’}=λ²⋅t_{‘A’B’C’D’E’}.
A gúlák testmagasságainak aránya is λ. Tehát: m’:m=λ.

Az A’B’C’D’E’T’ gúla térfogata: ​\( V_{A’B’C’D’T’}=\frac{t’·m’}{3}=\frac{λ^{2}t·λ·m}3=λ^{3}·V_{ABCDT} \)​ .

Tehát a két hasonló gúla térfogatának az aránya a hasonlóság arányszámának a köbével egyenlő: V_{A’B’C’D’T’} :V_ABCDT=λ³.

Megjegyzés: Belátható, hogy bármely két hasonló test térfogata között ugyanez az összefüggés áll fenn.