Adott egy háromszög három csúcspontjának koordinátái:
A(x1;y1), B(x2;y2), és C(x3;y3), helyvektoraik: \( \vec{a} \); \( \vec{b} \), és \( \vec{c} \).
Jelölje F(f1;f2) a BC oldal felezési pontját, S(s1;s2) pedig a háromszög súlypontját.
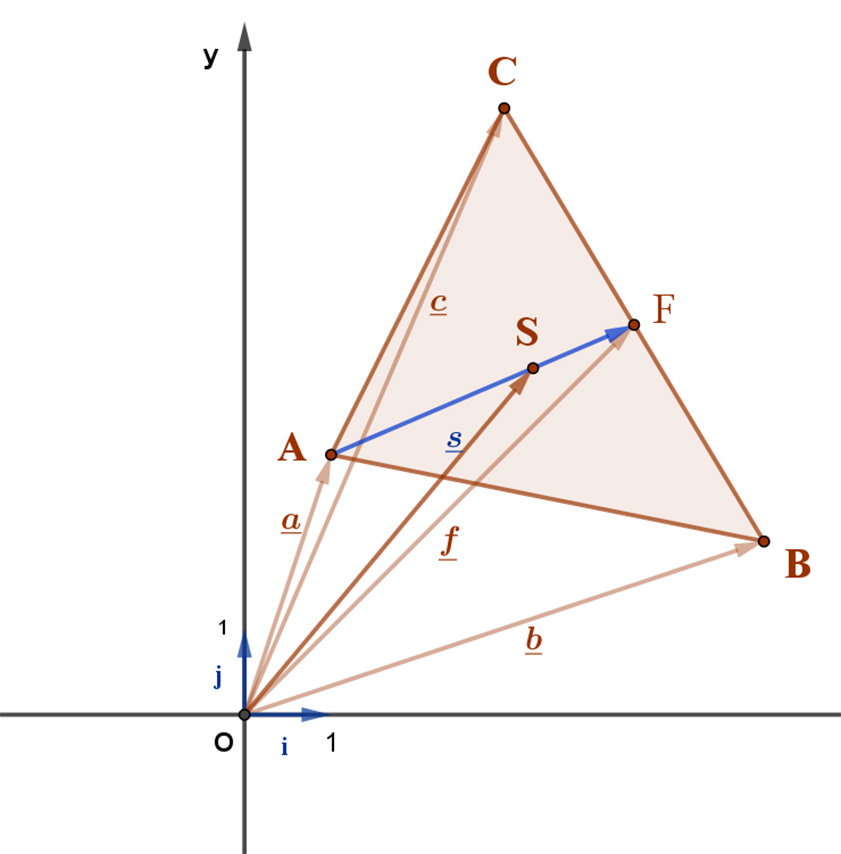
F pont helyvektorára felírható a felezési pontra vonatkozó alábbi vektoregyenlet: \( \vec{f}=\frac{(\vec{b}+\vec{c})}{2} \).
Ez alapján F pont koordinátái: \( f_{1}=\frac{x_{2}+x_{3}}{2} \) és \( f_{2}=\frac{y_{2}+y_{3}}{2} \).
Tudjuk, hogy a háromszög súlypontja harmadolja az AF súlyvonalat. Így S súlypont s helyvektorára felírható a harmadoló pontra vonatkozó vektoregyenlet: \( \vec{s}=\frac{\vec{a}+2\vec{f}}{3} \)==>\( \vec{s}=\frac{\vec{a}+\vec{b}+\vec{c}}{3} \).
Így tehát S súlypont koordinátáira: \( s_{1}=\frac{x_{1}+x_{2}+x_{3}}{3} \) és \( s_{2}=\frac{y_{1}+y_{2}+y_{3}}{3} \).
Feladat:
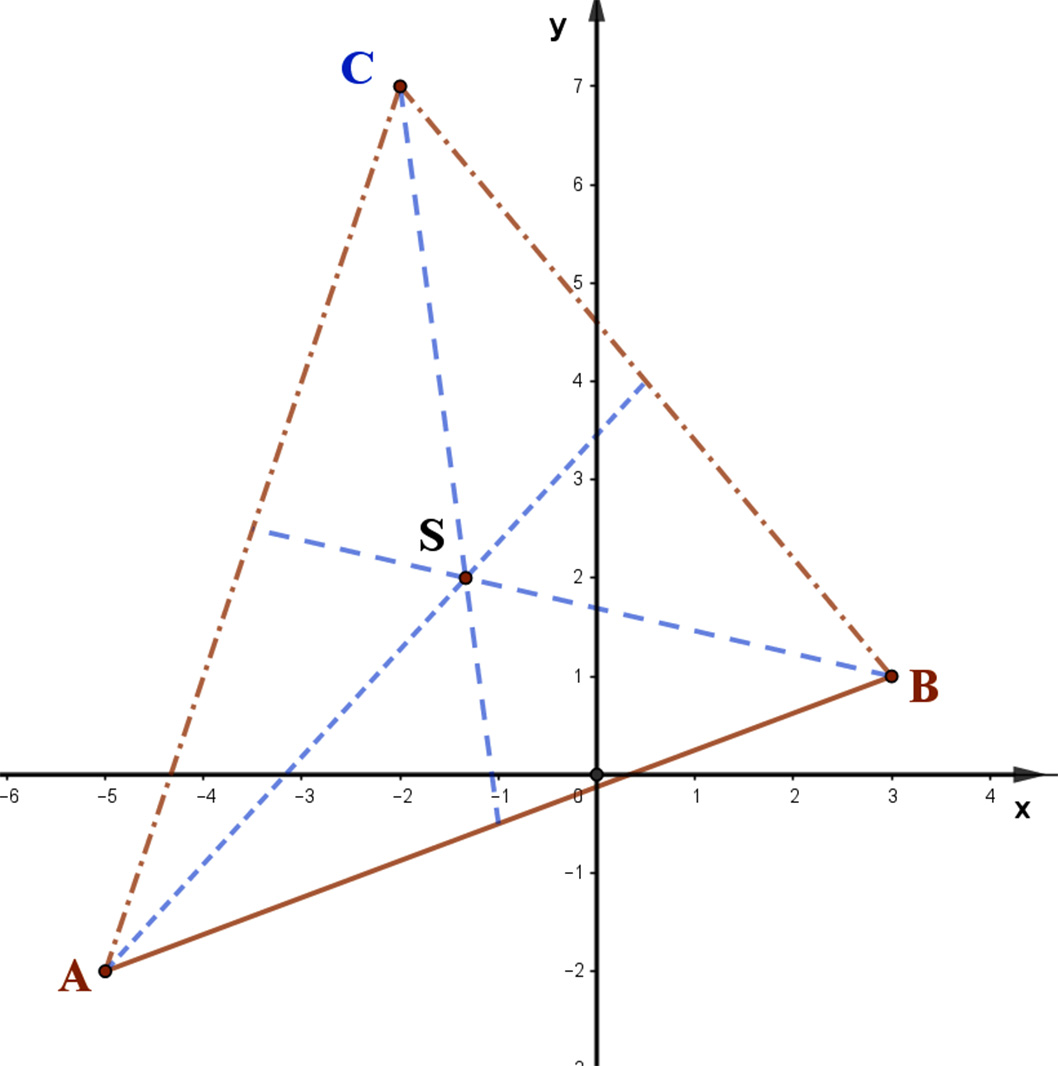
Egy háromszög két csúcspontjának koordinátái: A(-5;-2), és B(3;1). Súlypontja, S(-4/3;2). Írja fel a C csúcs koordinátáit!
(Összefoglaló feladatgyűjtemény 3246. feladat.)
Megoldás:
Jelöljük a keresett C pont koordinátáit: C(c1;c2).
Helyettesítsük be a fenti összefüggésbe a megadott pontok és a keresett pont koordinátáit!
\( -\frac{4}{3}=\frac{-5+3+c_{1}}{3} \) és \( 2=\frac{-2+1+c_{2}}{3} \).
3-mal átszorozva: -4=-5+3+c1 és 6=-2+1+c2.
c1-re és c2-re kifejezve: c1=-4+5-3=-2 és c2=6+2-1=7.
Tehát a keresett C pont koordinátái: C(-2;7).


Comments are closed, but trackbacks and pingbacks are open.