Halmazok elemszámát tekintve alapvetően két eset van:
1. Véges elemszámú halmazok számosságán elemeinek számát értjük.
2. Végtelen elemszámú halmazok.
Végtelen elemszámú halmazok
A halmazelmélet megalapozója és megteremtője az 1870-es években a német Cantor volt. Ő a halmazokat úgy vizsgálta, hogy azokat függetlenítette elemeinek sajátosságaitól.
Cantor gondolatai a végtelen valóságos létezésének meggyőződéséből fakadtak. Úgy gondolta, hogy végtelen elemszámú halmazok között is értelmezhetők az ugyanakkora, kisebb, nagyobb fogalmak. A végtelen halmazok számosságának a vizsgálatához egy teljesen új szemléletet adott.
A végtelen halmazokkal kapcsolatban elsőként azt a gondolatot vetette fel, hogy két halmaz egyenlő számosságú, ha elemei között kölcsönösen egyértelmű megfeleltetés létesíthető (elemei párba állíthatók).
Tekintsük alapként a ℤ+={Pozitív egészek számok} halmazát. Azt természetesnek tekintjük, hogy a ℤ–={Negatív egész számok} halmaza ugyanakkora számosságú. Hiszen minden ℤ+-beli elemhez hozzárendelhető egy ℤ–-beli elem, az ő ellentettje.
Az azonban már igen elgondolkoztató, hogy a P={Pozitív páros számok} halmaza is ugyanakkora számosságú, mint a pozitív egész számoké. Hiszen minden ℤ+-beli elemhez hozzárendelhető az ő kétszerese. Azaz:
| ℤ+={pozitív egész számok} | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … | n | … |
| P={páros számok} | 2 | 4 | 6 | 8 | 10 | 12 | 14 | … | 2n | … |
Párba állíthatók a természetes számok és a pozitív egész számok halmaza is.
| ℕ={természetes számok} | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … | n | … |
| ℤ+={pozitív egész számok} | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … | n+1 | … |
Ugyanígy kölcsönösen egyértelmű megfeleltetés létesíthető a pozitív egész számok (ℤ+) és a prímszámok (törzsszámok) (T) között:
| ℤ+={pozitív egész számok} | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … | n | … |
| T={Prímszámok} | 2 | 3 | 5 | 7 | 11 | 13 | 17 | … | n-edik prímszám | … |
A fenti halmazok tehát ugyanakkora számosságúak, hiszen mint láttuk, párba állíthatóak, pedig a ℤ+ halmaz tartalmazza T halmaz minden elemét és a ℤ+ valódi részhalmaza a ℤ halmaznak. T⊂ℤ+⊂ℕ⊂ℤ. A végtelen világa különös világ.
Cantor a pozitív egész számok halmazát és minden evvel azonos számosságú halmazt megszámlálhatóan végtelen számosságú halmaznak nevezett.
Definíció:
Ha valamely „H” halmaz elemei és a természetes számok között kölcsönösen egyértelmű hozzárendelést létesíthetünk, akkor a „H” halmazt megszámlálhatóan végtelen számosságú halmaznak nevezzük.
Tehát a fenti példákban szereplő számhalmazok (ℤ+; ℤ–;ℕ; P; T) számosságát tekintve egyenlők: megszámlálhatóan végtelen számosságúak.
Egy megszámlálhatóan végtelen halmaz minden végtelen részhalmaza is megszámlálható.
A fenti példáknál is különösebb, hogy a ℚ={Racionális számok} halmaza is „csak” megszámlálhatóan végtelen, azaz minden racionális számhoz hozzárendelhető egy pozitív egész szám, és minden pozitív egész számhoz csak egy racionális számot rendelünk.
Pedig a fenti halmazoknál még beszélhetünk szomszédos elemekről, ezt azonban a Q halmaz esetében nem mondhatjuk. Könnyen belátható, hogy bármelyik két racionális szám, bármelyik két törtszám közé végtelen sok törtszám illeszthető. (A racionális számok halmaza sűrű.)
Belátható, hogy elegendő csak a pozitív racionális számok, a ℚ+ halmaz számosságát vizsgálni.
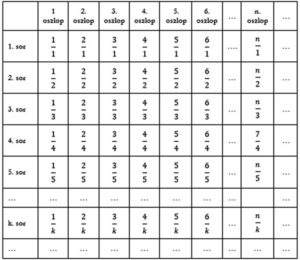Minden pozitív racionális szám \( \frac{m}{n} \) alakú, ahol m, n∈ ℤ+. Helyezzük el a pozitív racionális számokat egy táblázatba: A táblázat első sorában az 1 nevezőjű egész számok, a második sorban a n=2 nevezőjű racionális számokat írjuk És így tovább. Ebben a táblázatban minden pozitív racionális szám szerepel, igaz, többször (végtelen sokszor) is.
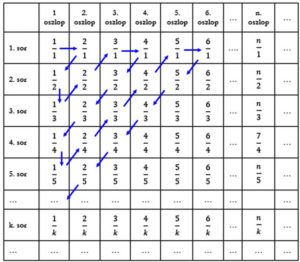
Most ugyanezt a táblázatot rendeljük hozzá a pozitív egész számokhoz az alábbi módon:
Azaz átlósan járjuk be az első táblázatot, és közben számlálunk.
A ℤ+ és a ℚ+ halmazok elemei párba állíthatók, tehát minden pozitív egész számhoz tartozik egy racionális szám.
| Z+:(lépésszám) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| Q+:={pozitív racionális számok} | 1 | \( \frac{2}{1} \) | \( \frac{1}{2} \) | \( \frac{1}{3} \) | \( \frac{2}{2} \) | \( \frac{3}{1} \) | \( \frac{4}{1} \) | \( \frac{3}{2} \) | … |
Megjegyzés: Ha a fenti táblázatban minden racionális számot csak egyszer írunk be (például úgy, hogy az \( \frac{m}{n} \) tört alakban az m és n egymáshoz képest relatív prímek legyenek.), akkor is megszámlálható halmazt kapunk.
Megszámlálhatóan végtelen halmazok tehát például:
Természetes számok
Pozitív egész számok
Egész számok
Prímszámok
Pozitív, páros egész számok
Pozitív, páratlan egész számok
Racionális számok
Vannak azonban nem megszámlálhatóan végtelen halmazok is, azaz amelyeknek elemei és a természetes számok között nem létesíthető egyértelmű hozzárendelés.
Ilyen például a valós számok (ℝ) halmaza.
Ennek a halmaznak a számosságát kontinuumnyi számosságúnak mondjuk. (Elnevezés: continuus: szakadatlan; folytonos.)
Kontinuumnyi számosságú a valós számhalmazok bármely intervalluma is, így a [0;1 ] intervallumban lévő valós számok száma halmaza is nem megszámlálhatóan végtelen számosságú halmaz.
https://hu.wikipedia.org/wiki/Sz%C3%A1moss%C3%A1g
http://www.math.u-szeged.hu/~hajnal/courses/Univ_Halmazelmelet/halmaz99/continu.htm
Comments are closed, but trackbacks and pingbacks are open.