Tétel: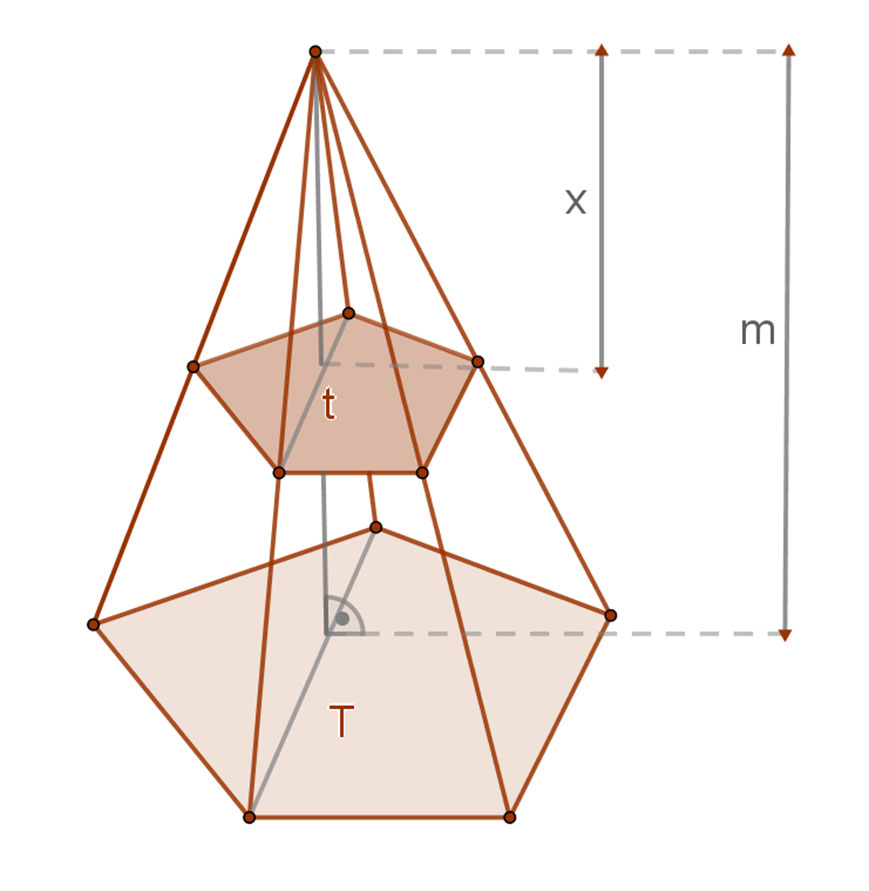
A gúla alappal párhuzamos síkmetszetének területe úgy aránylik a gúla alapterületéhez, mint ahogy a síkmetszetnek a gúla csúcsától mért távolságának a négyzete aránylik a gúla magasságához.
Jelöléssel: A mellékelt ábra jelölései szerint: t:T=x2:m2.
Bizonyítás:
A két síkidom –a t alapterületű síkmetszet, és a gúla T területű alaplapja– a gúla csúcsára nézve középpontosan hasonló.
A hasonlóság aránya megegyezik az alaplappal párhuzamos síkmetszet éleinek és a gúla alaplapja megfelelő éleinek arányával. Ez az arány egyenlő a síkmetszetnek a gúla csúcsától mért távolságának (x) és a gúla magasságának (m) az arányával, amely: x:m.
Tudjuk, hogy hasonló síkidomok területének aránya a hasonlósági arány négyzete.
Ezért a gúla alaplappal párhuzamos síkmetszetének a területe úgy aránylik a gúla alapterületéhez, mint a csúcstól számított távolságaik négyzete. Jelöléssel: t:T=x2:m2.


Comments are closed, but trackbacks and pingbacks are open.