A geometria szó a földmérés görög elnevezése. Ma a matematika egyik szakterületét jelenti elsősorban. Az ókorban többek között a kínaiaktól, a babilóniaiaktól, az egyiptomiaktól is maradtak fenn geometria feladatok, ismeretek, de a geometriát tudománnyá az ókori nagy görög matematikusok tették.
1. Fogalmak, alapfogalmak
Melyik a kakukktojás az alábbiak közül?
Pont, egyenes, sík, szakasz, vonal, felület, tér.
Persze, különböző szempontokból nézve talán nem egyértelmű a kérdés. De ha azt mondjuk, hogy a szakasz a kakukktojás, talán meg tudod indokolni!
A fent soroltak közül egyedül a szakasz fogalmát lehet meghatározni. A szakasz az egyenesnek két pont által határolt része. De hogy mi a pont, az egyenes, a vonal, a sík, a felület, a tér, vagy hogy mit értünk illeszkedésen, ezekre bizony nincs elfogadható definíció.
Lehet rájuk olyanokat mondani, hogy: a pont olyan, mint a tű hegye, és így tovább, de ezek nem meghatározások, csak hasonlatok. A matematika, és ezen belül a geometria is azokat a fogalmakat, amelyeket definiálni nem tud, de a körülöttünk lévő világból absztrakció útján mégis megalkot és használ, alapfogalmaknak nevezi.
Az alapfogalmakból kiindulva már tudunk pontos definíciókat adni, mint ahogy a szakasznál láttuk.
2. Állítások, axiómák
A geometriában a fogalmakkal kapcsolatban állításokat fogalmazunk meg. Például:
- A derékszögű háromszög befogóira emelt négyzetek területeinek összege egyenlő az átfogóra emelt négyzet területével. (Pitagorasz tétele.)
- Ha egy kör átmérőjének két végpontját összekötjük a kör bármely más pontjával, akkor derékszögű háromszöget kapunk. (Thalész tétele.)
- Két különböző pontra egy és csak egy egyenes illeszthető.
- Ha egy négyszög húrnégyszög, akkor szemközti szögeinek összege 180°. (Húrnégyszögek tétele 1.)
Ezek között az állítások között is van kakukktojás. A 3. állítást nem tudjuk bizonyítani, csak szemlélet alapján elfogadni.
A matematika és így a geometria is minden állítást bizonyítani szeretne. De ezen közben már az ókorban eljutottak annak felismerésére, hogy a legegyszerűbb állításokat már nem lehet bizonyítani. Az ilyen alapvető, és bizonyítás nélkül igaznak tekintett állításokat nevezzük axiómáknak. Persze mindig, minden szakterületen arra kell törekedni, hogy minél kevesebb ilyen alapállítás legyen.
Az ókori görögöknél Eukleidész ezeket az alapállításokat és alapfogalmakat rendszerezte. Az általa felállított axiómák közül egy különösen nevezetes: a párhuzamossági axióma, amely így szól:
Ha két, azonos síkban fekvő egyenes egy harmadik metsz, akkor a két egyenes a harmadiknak azon az oldalán metszi egymást, amelyiken a keletkezett belső szögek összege két derékszögnél kisebb.
Ez a párhuzamossági axióma sok okozott gondot majd 2000 éven át a matematikusoknak. Elsősorban bonyolultsága és ellenőrizhetetlensége miatt. Ez indította el az axiómarendszerekre vonatkozó vizsgálatokat. És ezekből a kutatásokból, illetve a párhuzamossági axióma tagadásából született meg a Bolyai-Lobacsevszkij féle geometria. Ők ezt a párhuzamossági axiómát annak tagadásával helyettesítették a következő módon:
Az „e” egyeneshez egy külső P pontból több olyan egyenes húzható az „e” és P által meghatározott síkban, amely e-t nem metszi.”
Ma már tudjuk, mindkét axiómát el lehet igaznak fogadni!
3. Térelemek kölcsönös helyzete
A következő térelemek kölcsönös helyzetét vizsgáljuk meg: pont, egyenes és sík.
Pont-pont kölcsönös helyzete. Két pont vagy illeszkedik (egybeesik), vagy nem.
Pont-egyenes kölcsönös helyzete. Pont az egyenesre vagy illeszkedik, vagy nem.
Pont-sík kölcsönös helyzete. Pont a síkra vagy illeszkedik, vagy nem.
Egyenes-egyenes kölcsönös helyzete. Két egyenes egymáshoz képest vagy illeszkedik (egybeesik) vagy nem.
Két különböző egyenesnek vagy van közös pontja, vagy nincs.
Ha két különböző egyenesnek van közös pontja (metsző egyenesek), akkor azok egy síkot határoznak meg.
Ha két különböző egyenesnek nincs közös pontja, akkor vagy van olyan sík, amelyik mindkettőt tartalmazza, vagy nincs.
Ha két különböző egyenesnek nincs közös pontja, de van olyan sík, amelyik mindkettőt tartalmazza, ezek a párhuzamos egyenesek.
Ha két különböző egyenesnek nincs közös pontja, és nincs olyan sík, amelyik mindkettőt tartalmazná, akkor ezek az egyenesek kitérők.
Egyenes-sík kölcsönös helyzete. Az egyenes vagy illeszkedik a síkra (rajta van), vagy nem. Ha az egyenes nem illeszkedik a síkra, akkor vagy van vele közös pontja (döfi) vagy nem, ekkor párhuzamos vele.
Sík-sík kölcsönös helyzete. Két sík vagy illeszkedik egymásra, vagy nem. Ha két sík nem illeszkedik egymásra, akkor vagy van közös pontjuk (metsző síkok), vagy nem. Ez utóbbi esetben a két sík párhuzamos. Ha két sík nem illeszkedik és van közös pontjuk, azaz metszik egymást, akkor közös pontjaik egy egyenest határoznak meg. (metszésvonal).
4. Távolság fogalma:
A távolság fogalma szorosan kötődik a mérés, és így az egység fogalmához. Egy adott szakaszt egységnyi hosszúságúnak tekinthetünk. A hétköznapi életben igen sokféle módon tesszük ezt. (méter, yard, könyök, stb.)
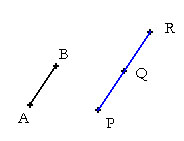Legyen a mellékelt ábrán az A és B pontok távolsága egységnyi, azaz AB szakasz hossza 1.
Ezt így jelöljük: d(A;B)=1
A mellékelt ábrán P és R pontok távolsága 2, azaz d(P;R)=2, mert az AB szakasz éppen kétszer mérhető rá.
A távolság fogalmáról többet megtudhatsz itt.
5. Szög fogalma
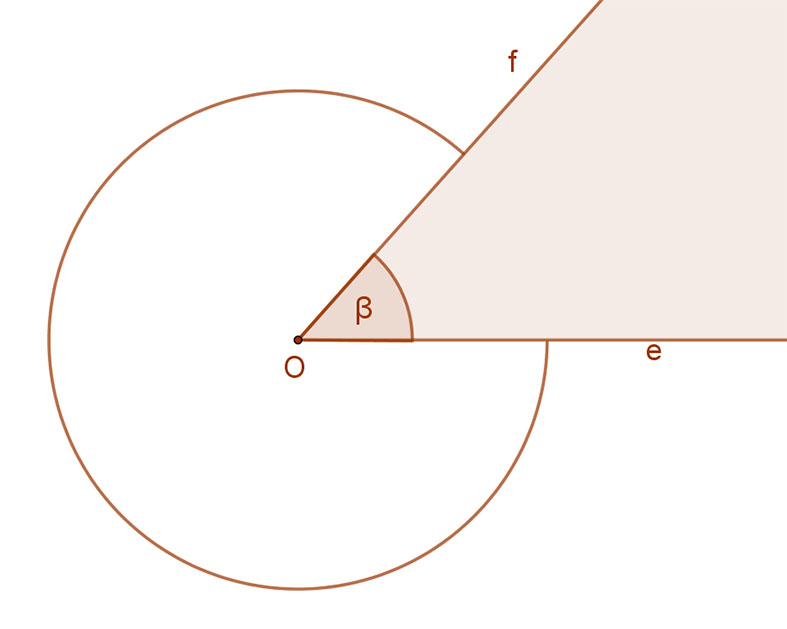Az egy pontból kiinduló két félegyenes a rájuk illeszkedő síkot két tartományra, két részre bontja. Ezeket a részeket szögtartományoknak nevezzük. A két félegyenes (e, és f) tehát két szögtartományt, vagy röviden két szöget hoz létre. A két félegyenest a szög szárainak, közös kezdőpontjukat (O) a szög csúcsának nevezzük. A szögeket a görög abc kis betűivel azonosítjuk, és egy körívvel jelöljük.
A szög létrejöttét felfoghatjuk úgy is, hogy egy félegyenest végpontja körül elforgatunk. Az így kapott síktartományt, azaz szöget forgásszögnek is mondjuk. Ebben az esetben a forgatás mértékén kívül a forgatás iránya is jellemző a szögre. Megegyezés szerint pozitív forgásiránynak az óramutató járásával ellentétes irányt értjük.
Az egymáshoz képest speciális (sajátos) helyzetű szögeket szögpároknak mondjuk.
6. Geometriai szerkesztésről
A geometria egyik szép területe a szerkesztés. Már az ókori matematikusokat is foglalkoztatta bizonyos tulajdonsággal rendelkező pontok (mértani helyek) előállítása szerkesztés útján. Ismét csak Eukleidész volt az, aki ezt a kérdést rendszerezte, szabályozta. Az általa felállított követelményeket ma is érvényben lévőnek tekintjük. Euklideszi módon adott egység ismeretében a \( \sqrt{2} \)hosszúságú szakasz szerkeszthető, de nem szerkeszthető a \( \sqrt[3]{2} \) hosszúságú szakasz, vagy a π hosszúságú szakasz. A kúpszeletek közül szerkeszthető a kör, de nem szerkeszthető az ellipszis, a parabola, illetve a hiperbola. Ezeknek a kúpszeleteknek véges számú pontja megszerkeszthető a fent értelemben, de a görbék nem. Ugyancsak nem végezhető el euklideszi módon például a szögharmadolás sem.
Érdekes matematikai probléma, ha azt keressük, hogy bizonyos eszközök birtokában, és azok meghatározott módon történő használatával mely szerkesztési feladatok végezhetők el és melyek nem.
Comments are closed, but trackbacks and pingbacks are open.