Bevezető feladat:
Vizsgáljuk meg az \( f(x)=\frac{x^2-9}{x-3} \) x∈ℝ|x≠3 függvényt.
Az a2-b2=(a+b)⋅(a-b) azonosság segítségével írjuk fel a számlálót szorzat alakban: \( f(x)=\frac{x^2-9}{x-3}=\frac{(x-3)(x+3)}{x-3} \).
Egyszerűsítés után a megadott függvény: f(x)=x+3; x∈ℝ|x≠3.
Ez a függvény egy egyszerű lineáris függvény, amely azonban x0=3 helyen nincs értelmezve.
A függvény grafikonja egy „lyukas” egyenes az x=3 pontban.
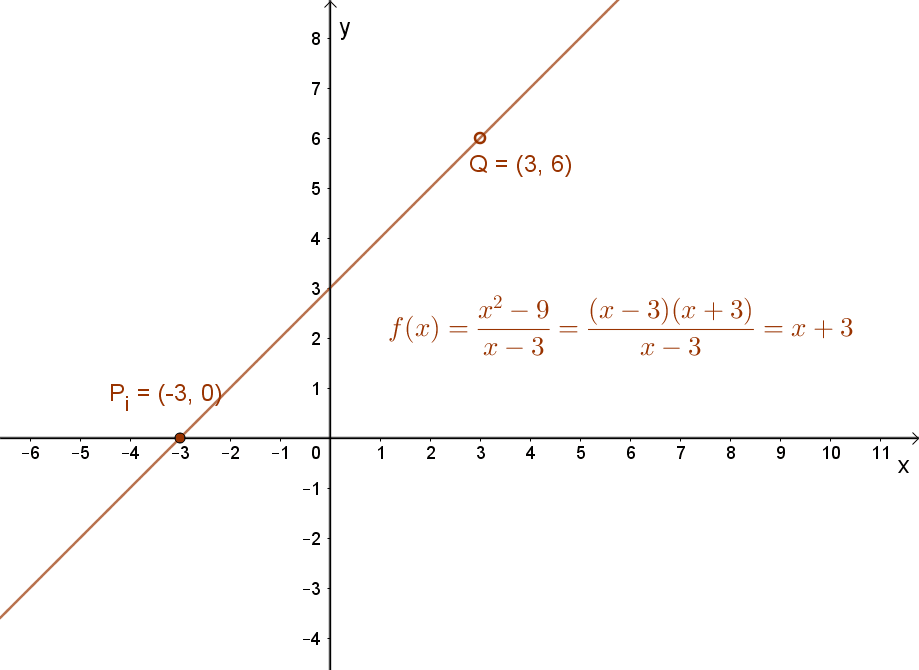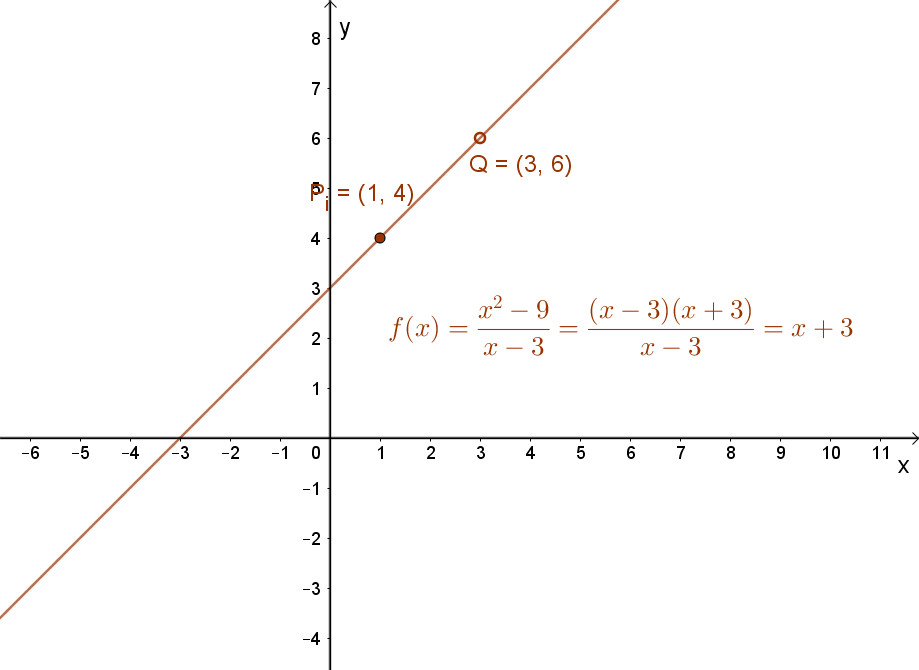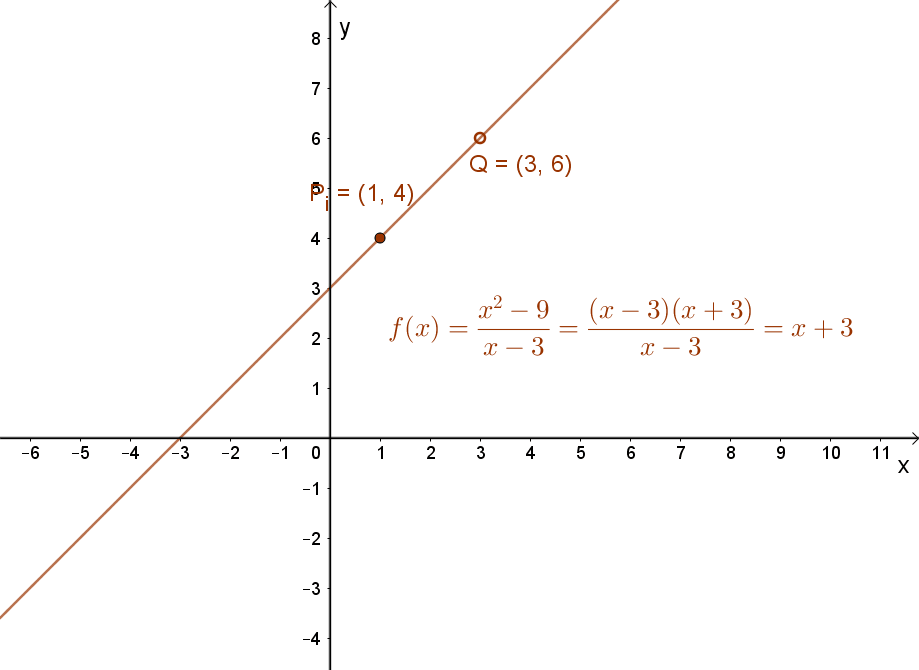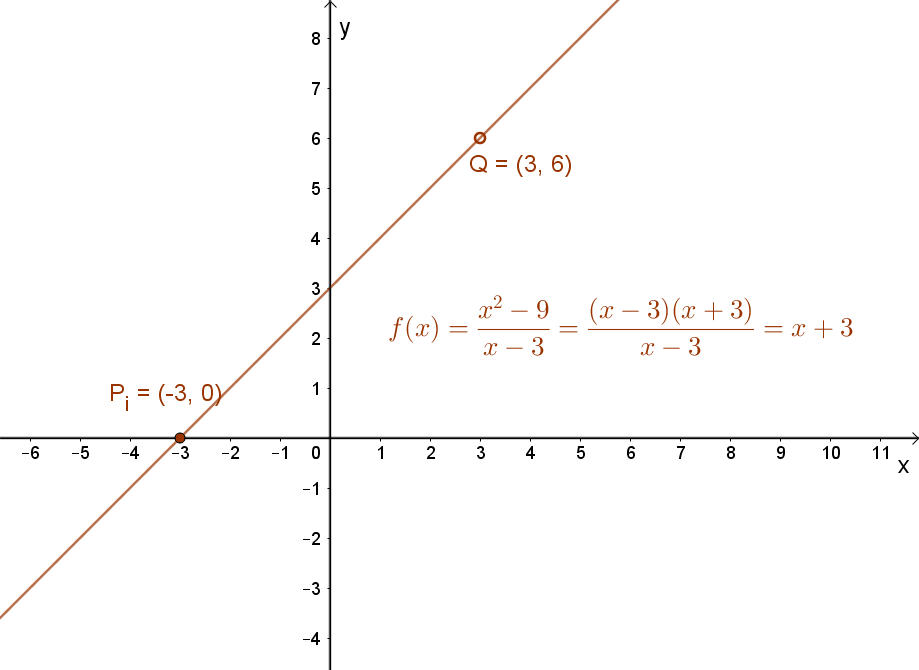
A számsorozatoknál már megismert határérték definíció felhasználásával lehet választ adni arra, hogy beszélhetünk-e ennek a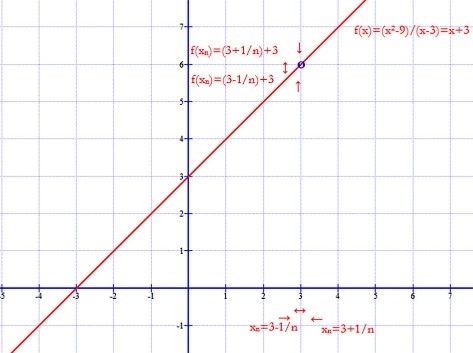 
függvénynek határértékéről, ha a függvény „x”változójával az x0=3 érték felé közeledünk.
Tekintsük a következő sorozatot \( x_{n}=\left(3+\frac{(-1)^n}{n}\right) \)! Ez a sorozat két oldalról közelít a 3-hoz. Ennek a sorozatnak a határértéke: \( \lim_{n\to \infty }\left(3+\frac{(-1)^n}{n}\right)=3 \).
Nézzük most az \( f(x_{n})=\left(3+\frac{(-1)^n}{n}+3\right) \) sorozatot! A függvényértékek sorozata két oldalról közeledik a 6-hoz.
\( \lim_{ n \to \infty }f(x_{n})=\lim_{n\to \infty }f(x_{n})=\left(3+\frac{(-1)^n}{n}+3\right)=6 \).
Függvény véges helyen vett határértéke.
Definíció:
Legyen az f(x) függvény értelmezve az x0 pont egy környezetében, kivéve esetleg az x0 pontot. Az f(x) függvénynek létezik az x0 pontban határértéke és ez „A”, ha bármely olyan xn sorozatra, amelynek tagjai elemei az f(x) függvény értelmezési tartományának és xn→x0, akkor a megfelelő függvényértékre f(xn)→A.
(Heine féle definíció).
Jelölés: \( \lim_{x→x_{0}}f(x)=A \).
A függvény pontbeli folytonossága nagyon szorosan kötődik a határérték fogalmához. Ezért mondhatjuk más megfogalmazásban a Heine féle definíciót:
Egy „f” függvény az értelmezési tartományának egy x0 elemében (pontjában) folytonos, ha az x0 helyen van határértéke és ez megegyezik a függvény helyettesítési értékével, vagyis \( \lim_{x→x_{0}}f(x)=f(x_{0}) \).
Határérték definíciójának másik megfogalmazása:
Legyen az f(x) függvény értelmezve az x0 pont egy környezetében, kivéve esetleg az x0 pontot. Az f(x) függvénynek létezik az x0 pontban határértéke és ez „A”, ha bármely (∀) ε>0-hoz létezik (∃) olyan δ>0, hogy ha 0<|x-x0|<δ, akkor |f(x)-A|<ε. (Cauchy féle definíció)
Jelölés: \( \lim_{x→x_{0}}f(x)=A \).
A fenti példa esetén: \( \lim_{x→3}\frac{x^2-9}{x-3}=6 \).
Tétel:
Függvények adott pontbeli (véges helyen vett) határértékeinek Heine illetve Cauchy féle definíciói ekvivalensek egymással.
Feladat
Legyen adott az m(x)=-x2 x∈R|x<0 és a g(x)=√x+1 függvények. Képezzük az f(x)=m(x)+g(x) függvényt! Ábrázoljuk és vizsgáljuk az f(x) függvényt határérték szempontjából az x0=0 pontban!
Megoldás:
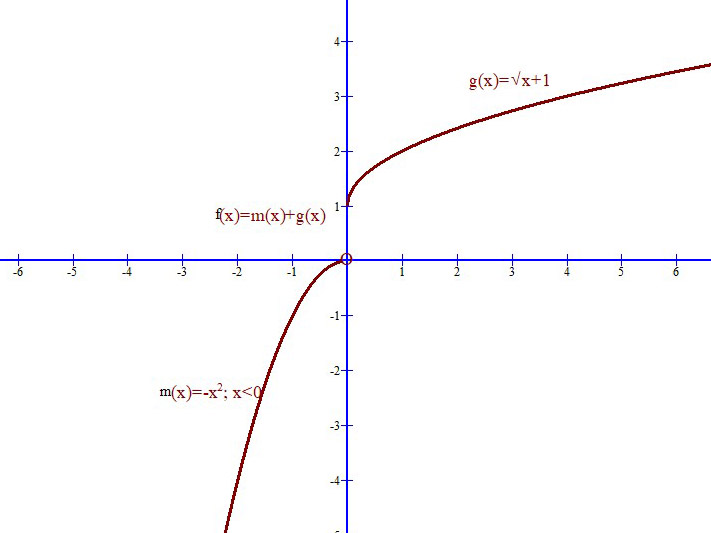Az f(x) függvény grafikonja:
Ha az x változóval jobbról közeledünk az x0=0 ponthoz a g(x)=√x+1 függvény mentén, akkor a függvényértékek sorozata az y=1-hez közeledik és f(0)=0.
Ha az x változóval balról közeledünk az x0=0 ponthoz az m(x)=-x2 függvény mentén, akkor a függvényértékek sorozata az y=0-hoz közeledik, bár f(o)=1=g(0), de az m(0) nincs értelmezve.
Ugyanakkor értelmezhető a függvények jobb illetve bal oldali határértéke.
Definíció:
Az f(x) függvénynek a valós x0 pontban jobb oldali határértéke „A”, ha az f(x) függvény az x0 valamely „I” jobb oldali környezetében és bármely \( {x^+_{n}} \)∈I, \( {x^+_{n}} \)→ x0 sorozat esetén \( f({x^+_{n}}) \)→A.
Az f(x) függvénynek a valós x0 pontban bal oldali határértéke „A”, ha az f(x) függvény az x0 valamely „I” bal oldali környezetében és bármely \( {x^-_{n}} \)∈I, \( {x^-_{n}} \)→ x0 sorozat esetén \( f({x^-_{n}}) \)→A.
Tétel:
Egy f(x) függvénynek akkor és csak akkor van egy adott x0 pontban határértéke, ha ott a jobb és bal oldali határérték is létezik és azok egyenlők.
Így a fenti f(x) függvénynek nincs határértéke x0=0 pontban, mivel a jobb és a bal oldali határértékek bár léteznek, de nem egyenlők.
Függvény határértékére vonatkozó legfontosabb tételek
1. Függvények számszorosára vonatkozóan:
Ha az x0 pontban \( \lim_{x→x_{0}}f(x)=A \), akkor \( \lim_{x→x_{0}}c·f(x)=c·A \) , ahol „c” egy adott valós szám.
2. Függvények összegére vonatkozóan:
Ha az x0 pontban \( \lim_{x→x_{0}}f(x)=A \) és \( \lim_{x→x_{0}}g(x)=B \), akkor \( \lim_{x \to x_{0} }\left [f(x)+g(x)\right ] =A+B \).
3. Függvények különbségére vonatkozóan:
Ha az x0 pontban \( \lim_{x→x_{0}}f(x)=A \) és \( \lim_{x→x_{0}}g(x)=B \) és , akkor \( \lim_{x \to x_{0} }\left [f(x)-g(x)\right ] =A-B \).
4. Függvények szorzatára vonatkozóan:⋅
Ha az x0 pontban \( \lim_{x→x_{0}}f(x)=A \) és \( \lim_{x→x_{0}}g(x)=B \), akkor \( \lim_{x \to x_{0} }\left [f(x)·g(x)\right ] =A·B \).
5. Függvények hányadosára vonatkozóan:
Ha az x0 pontban \( \lim_{x→x_{0}}f(x)=A \) és \( \lim_{x→x_{0}}g(x)=B \) , akkor \( \lim_{ x \to x_{0}}\frac{f(x)}{g(x)}=\frac{A}{B} \), feltételezve, hogy B≠0.
Comments are closed, but trackbacks and pingbacks are open.