Feladatok:
1. Legyen adott az a következő lineáris függvény: l(x)=0.5⋅x .
Ábrázoljuk és számítsuk ki a függvény alatti területet a [2,6] intervallumon!
Megoldás:
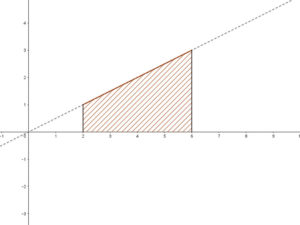A lineáris függvény alatti terület ezen az intervallumon egy trapéz. Így a területe a trapézokra vonatkozó terület képlettel könyen számítható: Ttrapéz= (1+3)⋅4/2=8 területegység.
Persze, a terület kiszámítása a határozott integrál segítségével sem nehéz. az l(x)=0.5⋅x függvény primitív függvénye: \( L(x)=\frac{1}{2}·\frac{x^{2}}{2}=0.25·x^{2} \).
Így
\[ \int_{2}^{6}{\frac{1}{2}x }dx=\left [F(x) \right ]_{2}^{6}=0.25\left [x^{2} \right ]_{2}^{6}=0.25·(36-4)=8 \]
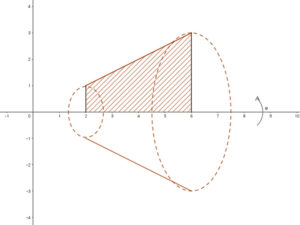
2. Forgassuk meg az l(x)=0.5⋅x függvényt az „x” tengely körül!
Milyen testet kapunk a [2;6] intervallumon? Számítsuk ki a forgástest térfogatát!
Megoldás:
Egy csonkakúpot kapunk, amelynek a térfogatát a csonkakúp térfogatára vonatkozó képlet segítségével ki tudjuk számítani. A csonkakúp alap és fedőkörének a sugara: l(2)=1, l(6)=3, a csonkakúp magassága az intervallum hossza m=4.
Így a csonkakúp térfogata: \( V_{csunkakúp}=\frac{4 π (3^{2}+3·1+1^{2})}{3}=\frac{52 π }{3}≈54.45 \).
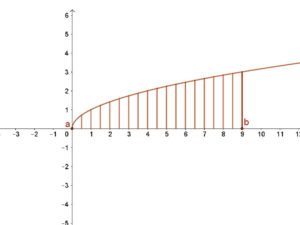
3. Legyen adott a g(x)=\( \sqrt{x} \) függvény.
Ábrázoljuk és számítsuk ki a függvény alatti területet a [0,9] intervallumon!
Megoldás:
Itt most nincs más választásunk, a határozott integrál integrál segítségével határozzuk meg a keresett értéket.
A g(x)=\( \sqrt{x} \) függvény primitív függvénye: \( G(x)=\frac{2}{3}\sqrt{x^{3}} \).
A keresett terület:
\[ \int_{0}^{9}{\sqrt{x}dx }=\left [\frac{2}{3}\sqrt{x^{3}} \right ]_{0}^{9}=\frac{2}{3}\sqrt{9^{3}}-\frac{2}{3}\sqrt{0^{3}}=\frac{2}{3}·3^{3}=18 \]
4. Feladat
Forgassuk meg a g(x)=\( \sqrt{x} \) függvényt az „x” tengely körül!
Milyen testet kapunk? Számítsuk ki a térfogatát a [0; 9] intervallumon!
Megoldás:
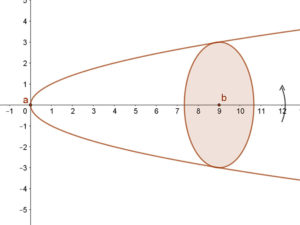A kapott test neve: forgásparaboloid. A térfogatát azonban „hagyományos” eszközökkel nem tudjuk kiszámítani.
Próbáljuk meg a területeknél már bevált módon és kezeljük a problémát általánosan.
Hasonlóan fogunk eljárni, mint a terület meghatározásánál és alkalmazzuk a kétoldali közelítés módszerét.
Tegyük fel, hogy egy f(x) függvény az [a;b] intervallumon folytonos továbbá, hogy f(x)≥0 az [a;b] intervallumon.
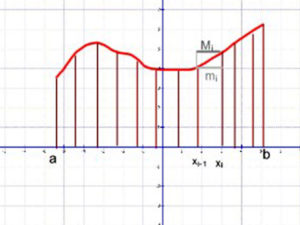
Osszuk fel az [a;b] intervallumot „n” részre és nézzük a beírt és a köréírt téglalapokat!
Az egyes téglalapok oldalai: az intervallum részintervallumai: xi – xi-1 és a részintervallumok végpontjaiban a függvényértékek a beírt téglalapnál: mi =f(xi-1), a köréírt téglalapnál: Mi =f(xi). (i = 1;2;…n; x0= a; és xn=b.)
Forgassuk meg a függvény a beírt és köréírt téglalapokkal együtt!
A forgatás után beírt és köréírt hengereket kapunk, amelyek magasságai a részintervallumok hosszai, a hengerek sugara pedig a részintervallumok végpontjaiban vett függvényértékek. Beírt hengereknél: ri=mi=f(xi-1), a köréírt hengereknél: Ri=Mi=f(xi).
A beírt hengerek térfogatainak összege:
\[ V_{beírt}=m^{2}_{1}(x_{1}-x_{0})+…+m^{2}_{i}(x_{i}-x_{i-1})+…+m^{2}_{n}(x_{n}-x_{n-1}) \].
Azaz:
\[ V_{beírt}=f^{2}(x_{0})π (x_{1}-x_{0})+…+f^{2}(x_{i-1}) π (x_{i}-x_{i-1})+…+f^{2}(x_{n-1}) π (x_{n}-x_{n-1}) \]
A köréírt hengerek térfogatainak összege:
\[ V_{köréírt}=M^{2}_{1} π (x_{1}-x_{0})+…+M^{2}_{i} π (x_{i}-x_{i-1})+…+M^{2}_{n} π (x_{n}-x_{n-1}) \].
Azaz:
\[ V_{köréírt}=f^{2}(x_{1})π (x_{1}-x_{0})+…+f^{2}(x_{i})π (x_{i}-x_{i-1})+…+f^{2}(x_{n})π (x_{n}-x_{n-1}) \]
A vbeírt és a Vköréírt a forgástest „V” térfogatát közrefogják, azaz vbeírt≤V ≤Vköréírt.
A vbeírt és a Vköréírt az f2 forgástest alsó és felső összegei.
Mivel az „f” függvény folytonos, ezért a f2π függvény is folytonos és integrálható.
Ebből következik, hogy egyetlen olyan szám van, amely minden „n”-re a [vbeírt;Vköréírt] intervallumba esik.
Ez a szám a vbeírt és Vköréírt sorozatok közös határértéke az \( π \int_{a}^{b}{ f^{2}(x)dx} \)szám.
Tehát az f(x) folytonos függvény által az [a;b] intervallumon meghatározott forgástest a térfogata:
\( V= π \int_{a}^{b}{ f^{2}(x)dx} \).
Nézzük most ennek a képletnek az alkalmazását a fenti példák esetén:
1. Az l(x)=0.5⋅x függvénynek a [2;6] intervallumon történt forgatása után egy csonkakúpot kaptunk.
Ennek térfogatát már kiszámoltuk hagyományos módon: : \( V_{csunkakúp}=\frac{4 π (3^{2}+3·1+1^{2})}{3}=\frac{52 π }{3}≈54.45 \).
Számoljuk most ki a fenti képlettel integrálás segítségével!
Az l(x)=0.5⋅x függvény négyzete: l2(x)=0.25x2 primitív függvénye: \( L(x)=0.25·\frac{x^{3}}{3} \).
A határozott integrál tehát: \( V= π \int_{2}^{6}{(0.5x)^{2}dx}=0.25 π \int_{2}^{6}{x^{2}dx} \).
Így \( V=0.25 π ·\left [\frac{x^{3}}{3} \right ]_{2}^{6}=0.25 π\left(\frac{6^{3}}{3}-\frac{2^{3}}{3} \right) =\frac{52 π }{3} \).
Ez az eredmény természetesen megegyezik a hagyományos módon kiszámolt értékkel.
2. Most már meg fogjuk tudni határozni a g(x)=\( \sqrt{x} \) függvénynek az „x” tengely körüli megforgatásával kapott forgásparaboloid térfogatát is.
Mivel g(x)=\( \sqrt{x} \), ezért g2(x)=x. Ennek primitív függvénye: \( G(x)=\frac{x^{2}}{2} \).
Így: \( V= π \int_{0}^{9}{\sqrt{x}^{2}dx}= π \int_{0}^{9}{ x}dx \).
Tehát: \( V= π ·\left [\frac{x^{2}}{2} \right ]_{2}^{6}= π ·\left( \frac{9^{2}}{2}-\frac{2^{2}}{2} \right) =\frac{81 π }{2}≈127.2 \) területegység.
Megjegyzés: A kapott összefüggés általánosítható.
Az \( y=\sqrt{2px} \) (x≥0) egyenletű görbének a az”x” tengely körüli megforgatásával a [0;m] intervallumon kapott „m” magasságú paraboloid térfogata: \( V= π\int_{0}^{m}{(\sqrt{2px})^{2} }=2p π \int_{0}^{m}{xdx } \).
Így \( V= 2pπ ·\left [\frac{x^{2}}{2} \right ]_{0}^{m}=pm^{2} π \).
Megjegyzés: Az \( y=\sqrt{2px} \) egyenletű görbe függvény, de az y2=2px egyenletű görbe nem függvény, bár az „x” tengely körüli forgatása ugyanazt a forgásparaboloidot adja.
Comments are closed, but trackbacks and pingbacks are open.