Hétköznapi értelemben két eseményt akkor nevezünk függetlennek, ha nincsenek egymásra befolyással, azaz az egyik bekövetkezése esetén a másik esemény bekövetkezésének az esélye sem nem nagyobb, sem nem kisebb.
o Ha két ember céltáblára lő, akkor a találatok egymástól függetlenek.
o Ha egy társasjátékban az a szabály, hogy csak 6-os dobással lehet kezdeni, akkor minden játékosnak 1/6 az esélye a kezdésre. Annak a valószínűsége, hogy a két játékos egymás után dobva ki tud lépni: 1/6⋅1/6/1/36. A valószínűségeik összeszorzódtak.
A feltételes valószínűség definíciója szerint: \( P(A|B)=\frac{P(A·B)}{P(B)} \). A P(AB)/P(B) hányados az „A” esemény bekövetkezésének a valószínűsége feltéve, hogy a „B” esemény is bekövetkezik.
Ha azonban feltételezzük, hogy a „B” esemény (feltétel) nem befolyásolja az „A” esemény bekövetkezését, akkor P(A|B) = P(A) egyenlőségnek fenn kell állnia.
De ha: \( P(A|B)=\frac{P(A·B)}{P(B)}=P(A) \), akkor a \( \frac{P(A·B)}{P(B)}=P(A) \) egyenlőségben a P(B) valószínűséggel átszorozva:
P(A⋅B)=P(A)⋅P(B).
Tehát a független események esetében a független események szorzatának valószínűsége megegyezik az egyes események valószínűségének a szorzatával.
Definíció:
A „H” eseménytéren értelmezett „A” és „B” eseményeket egymástól függetlennek mondjuk, ha P(A⋅B)=P(A)⋅P(B), azaz a független események szorzatának valószínűsége megegyezik az egyes események valószínűségének a szorzatával.
Ha az „A” esemény független „B”-től, akkor a „B” esemény is független „A”-tól. P(A⋅B)=P(A)⋅P(B) összefüggés a két esemény egymástól való függetlenségét is kifejezi.
Az események függetlenségének a definíciójára megadott fenti összefüggés másképp:
Ha „A” és „B” események függetlenek, akkor P(A|B)=P(A) és P(B|A)=P(B).
Megjegyzés:
Ha egy „A” eseményre P(A)=0 vagy P(A)=1, akkor az „A” esemény minden eseménytől független.
Az egymást kizáró események nem függetlenek! Ha két esemény kizárja egymást, akkor egymástól nem függetlenek. Egyik bekövetkezése hatással van a másikra. Az egyik miatt a másik nem következhet be.
Ha „A” és „B” események egymást kizáróak, akkor P(A⋅B)=0.
Nem szabad tehát összekeverni az egymást kizáró eseményeket /P(A⋅B)=0/ és az egymástól független eseményeket. /P(A⋅B)=P(A)⋅P(B)/.
A fogalom általánosítása:
A „H” eseménytéren értelmezett „A1”, „A2”,… „An” eseményeket egymástól teljesen függetlennek mondjuk, ha közülük bárhogyan kiválasztva „k” számú („Ai1”,„Ai2”,… „Aik”) eseményeket ezekre fennáll: P(Ai1⋅ Ai2⋅ …⋅ Aik)=P(Ai1)⋅P(Ai2)⋅…⋅P(Aik).
Tehát kettőnél több esemény függetlenségéhez nem elég, ha páronként függetlenek, mert összességükben még fennállhat közöttük kapcsolat
1. Feladat
Ketten lőnek céltáblára. Mivel a két célba lövő nem egyforma kvalitású, az egyik esetében a találat valószínűsége 0.7, míg a gyengébb lövész esetében 0.6. A találatok egymástól függetlenek. Ha mindketten egy-egy lövést adnak le , mennyi a valószínűsége annak, hogy legalább egy találat van a céltáblán?
Megoldás
„A” esemény: {A jobbik lövése talál}; „B” esemény: {A gyengébbik lövész talált},
Ekkor „A+B” az az esemény, hogy {Van találat a céltáblán}.
Mivel az „A” és „B” események egymástól függetlenek, ezért P(A⋅B)=P(A)⋅P(B).
Az események összegére vonatkozó jól ismert P(A+B)=P(A)+P(B )-P(AB) összefüggés szerint:
P(A+B)=0,7+0,6-0,7⋅0,6=1,3-0,42=0,88.
Tehát 0.88 valószínűséggel lesz találat a céltáblán!
2. Feladat
Egy kalapban 10 darab piros és 8 darab kék golyó van. Egymás után kihúzunk két golyót úgy, hogy az elsőnek kihúzott golyót nem tesszük vissza. Legyen „A” esemény, hogy az elsőnek kihúzott golyó piros, és legyen „B” esemény, hogy a másodiknak kihúzott golyó kék. Döntsük el, hogy az”A” és „B” események egymástól függetlenek-e!
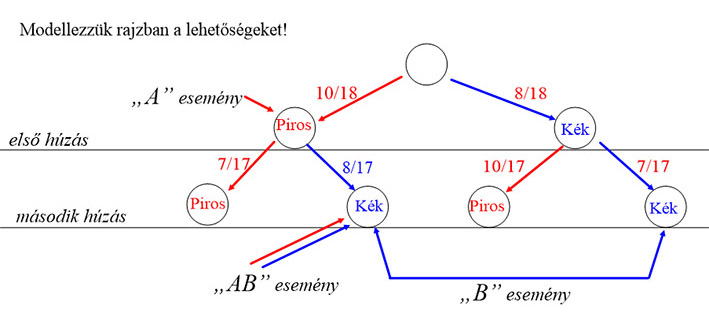
Az „A” esemény valószínűsége a feladat feltétele szerint: \( P(A)=\frac{10}{18} \).
Mivel az első golyót nem tettük vissza, ezért a második golyó kihúzásakor két eset van.
1. Ha az első húzáskor piros golyót húztunk, akkor a kék golyó húzásának a valószínűsége: \( \frac{10}{18}⋅\frac{8}{17} \).
2. Ha azonban az első golyó is kék volt, akkor a második húzásra \( \frac{8}{18}⋅\frac{7}{17} \) valószínűsége a kék golyó húzásának.
Így a „B” esemény valószínűsége: P(B)= \( \frac{10}{18}⋅\frac{8}{17} \) + \( \frac{8}{18}⋅\frac{7}{17} \) = \( \frac{136}{306} \) ≈0,4.
Az „A⋅B” esemény valószínűsége: P(AB)= \( \frac{10}{18}⋅\frac{8}{17} \)=\( \frac{80}{306} \)≈0.26.
Ugyanakkor a P(A)⋅P(B)= \( \frac{10}{18}⋅\frac{136}{306}=\frac{1360}{5508} \)≈0,24.
Mivel P(AB)≠P(A)⋅P(B), ezért az „A” és „B” események nem függetlenek egymástól.
Hiszen az első golyót a kihúzás után nem tettük vissza.
3. Feladat
Egy kalapban 10 darab piros és 8 darab kék golyó van. Egymás után kihúzunk két golyót úgy, hogy az elsőnek kihúzott golyót visszatesszük. Legyen „A” esemény, hogy az elsőnek kihúzott golyó piros, és legyen „B” esemény, hogy a másodiknak kihúzott golyó kék. Döntsük el, hogy az”A” és „B” események egymástól függetlenek-e!
Modellezzük rajzban a lehetőségeket!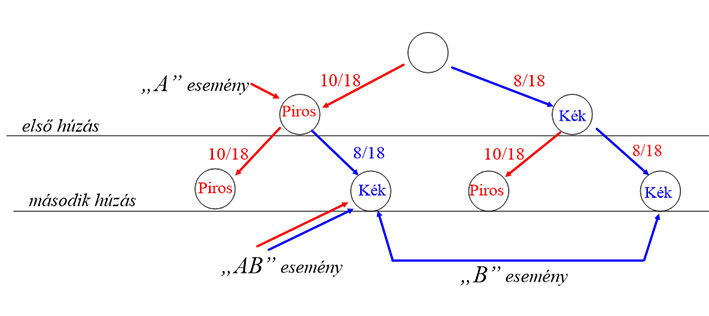
Az „A” esemény valószínűsége a feladat feltétele szerint most is: \( P(A)=\frac{10}{18} \).
Mivel az első golyót visszatettük, ezért a második golyó kihúzásakor függetlenül attól, hogy az első golyó piros vagy kék volt, mind a két esetben a valószínűség: \( \frac{10}{18}*\frac{8}{18} \).
Így a „B” esemény valószínűsége: P(B)= \( \frac{10}{18}*\frac{8}{18}+\frac{10}{18}*\frac{8}{18}=2*\frac{10}{18}*\frac{8}{18}=\frac{160}{324} \)≈0,49.
Az „A⋅B” esemény valószínűsége: P(AB)= \( \frac{10}{18}*\frac{160}{324}=\frac{1600}{5832} \)≈0,27.
Ugyanakkor P(A)⋅P(B)=\( \frac{10}{18}*\frac{160}{324}=\frac{1600}{5832} \)≈0,27.
Mivel P(AB)=P(A)⋅P(B), tehát az „A” és „B” események egymástól függetlenek.
Mivel az első golyót a kihúzás után visszatettük.


Comments are closed, but trackbacks and pingbacks are open.