Szakasz felezési pontjának meghatározása.
Adott az (xy) koordinátasíkon az A pont, helyvektora \( \vec{a} \), B pont helyvektora \( \vec{b} \).
Az AB szakasz F felezőpontjának helyvektora \( \vec{f} \). Ezt úgy kapjuk meg, ha az A pont helyvektorához hozzáadjuk az \( \overrightarrow{AB} \) vektor felét.
A mellékelt ábrán olvasható levezetés eredménye: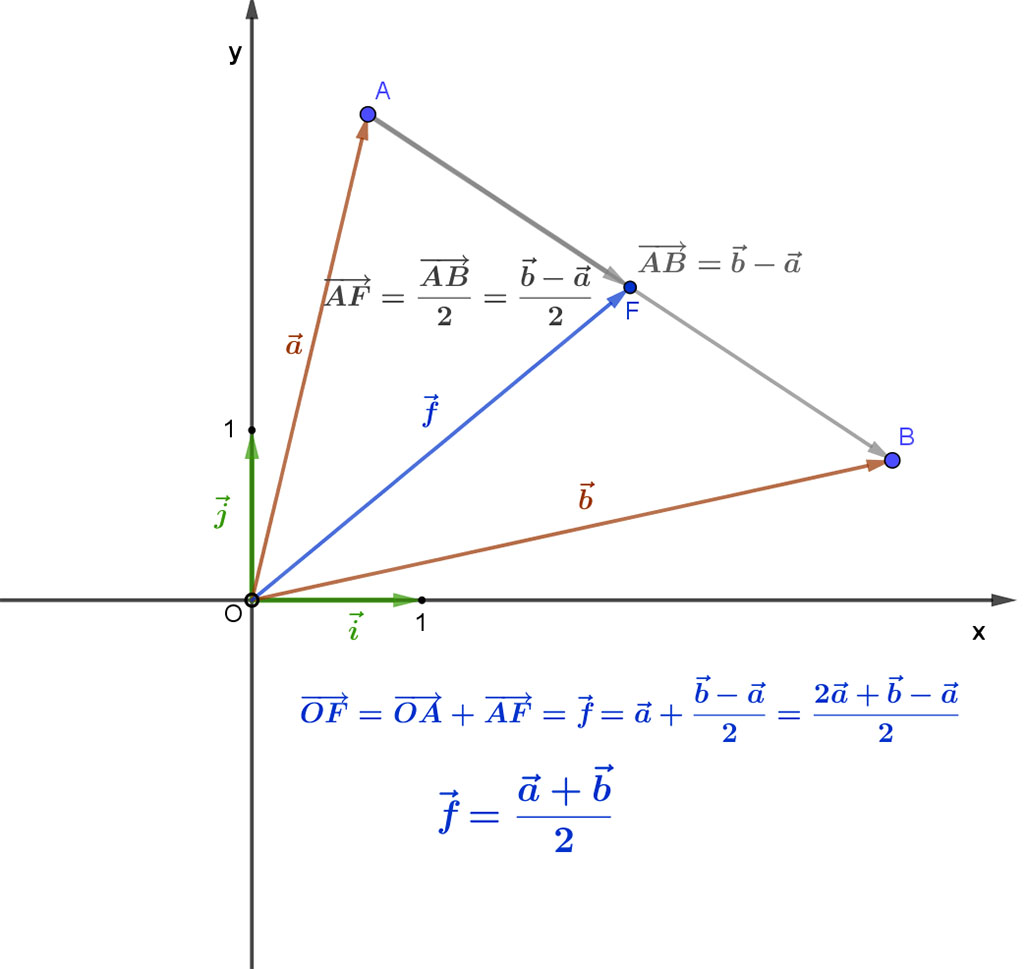
Az F pont helyvektora egyenlő az A és B pontok helyvektorainak összegének a felével.
Az A és B pontok koordinátáinak ismeretében az \( \vec{f}=\frac{(\vec{a}+\vec{b})}{2} \) vektoregyenletből kiszámíthatjuk az F felezési pont koordinátáit.
Ha A(x1;y1) és B(x2;y2)=> \( \overrightarrow{OA} \)= \( \vec{a} \)(x1;y1), \( \overrightarrow{OB} \) =\( \vec{b} \)(x2;y2), akkor \( \overrightarrow{OF}=\vec{f}=\left(\frac{x_{1}+x_{2}}{2};\frac{y_{1}+y_{2}}{2} \right) \).
Tehát a felezési pont koordinátái a határoló pontok megfelelő koordinátáinak számtani közepével egyenlők.
Szakasz harmadoló pontjának meghatározása:
Adott az (xy) koordinátasíkon az A pont, helyvektora \( \vec{a} \), B pont helyvektora \( \vec{b} \).
Az AB szakasz H1 (A-hoz közelebbi) harmadoló pontjának helyvektora \( \vec{h} \)1. Ezt úgy kapjuk meg, ha az A pont helyvektorához hozzáadjuk az vektor harmadát.
A mellékelt ábrán olvasható levezetés eredménye.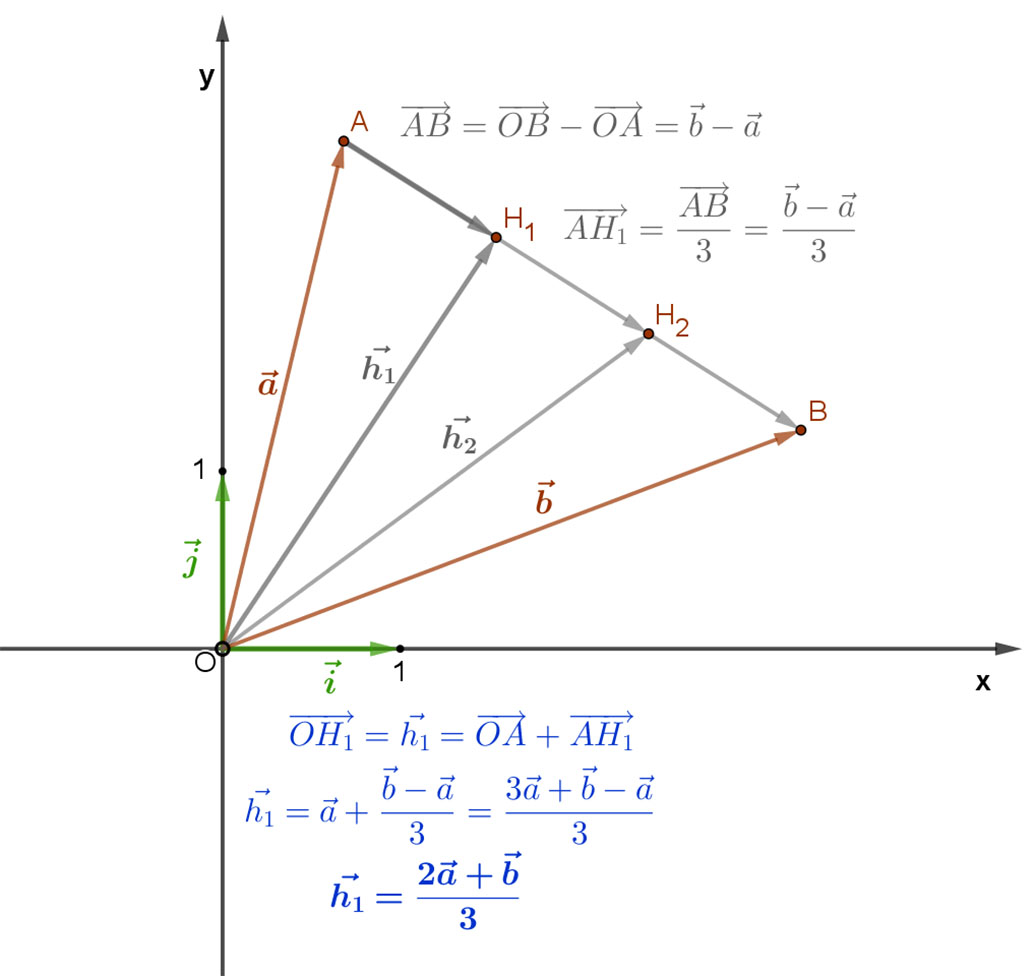 A H1 pont helyvektorát megkapjuk, ha az A pont helyvektorának kétszereséhez hozzáadjuk a B pontok helyvektorát, és az így kapott vektor 1/3 részét vesszük.
A H1 pont helyvektorát megkapjuk, ha az A pont helyvektorának kétszereséhez hozzáadjuk a B pontok helyvektorát, és az így kapott vektor 1/3 részét vesszük.
Az A és B pontok koordinátáinak ismeretében az \( \vec{f}=\frac{(2\vec{a}+\vec{b})}{3} \) vektoregyenletből kiszámíthatjuk az H1 harmadoló pont koordinátáit.
Ha A(x1;y1) és B(x2;y2)=> \( \overrightarrow{OA} \)= \( \vec{a} \)(x1;y1), \( \overrightarrow{OB} \) =\( \vec{b} \)(x2;y2), akkor \( \overrightarrow{OH_{1}}=\vec{f}=\left(\frac{2x_{1}+x_{2}}{3};\frac{2y_{1}+y_{2}}{3} \right) \).
Szakasz adott arányú osztása:
A harmadoló pont meghatározásához hasonlóan lehet egy adott szakaszt adott m:n arányban felosztani.
Az AB szakasz m:n arányú P osztópontjára, az egyes szakaszhosszúságokra: AP:PB=m:n.
Azaz AP:(AB-AP)=m:n. Ebből n⋅AP=m⋅(AB-AP) => n⋅AP+m⋅AP=m⋅AB => AP⋅(n+m)=m⋅AB. Tehát AP=m⋅AB/(m+n).
Így a P pont p helyvektorának felírásához a következő vektoregyenletet lehet felírni: p=a+m(b-a)/(m+n)
Itt az a vektor az A pont, a b vektor a B pont helyvektora, (\( \vec{b} \)-\( \vec{a} \) vektor pedig az A pontból a B pontba mutató szabadvektor.
Így a P pont helyvektorának felírásához a következő vektoregyenletet lehet felírni: \( \vec{p}=\vec{a}+\frac{m(\vec{b}-\vec{a})}{m+n} \).
Itt az \( \vec{a} \) vektor az A pont, a \( \vec{b} \) vektor a B pont helyvektora, (\( \vec{b} \)-\( \vec{a} \)) vektor pedig az A pontból a B pontba mutató szabadvektor.
A fenti vektoregyenletet átalakítva (közös nevezőre hozva): \( \vec{p}=\frac{(m+n)\vec{a}+m(\vec{b}-\vec{a})}{m+n} \).
Zárójelek felbontása után: \( \vec{p}=\frac{m\vec{a}+n\vec{a}+m\vec{b}-m\vec{a}}{m+n} \).
Összevonásokkal a kapott vektoregyenlet: \( \vec{p}=\frac{n\vec{a}+m\vec{b}}{m+n} \).
Ennek alapján A és B pontok koordinátáinak ismeretében a P pont első (x) koordinátája: \( x=\frac{nx_{1}+mx_{2}}{m+n} \) és a P pont második (y) koordinátája: \( y=\frac{ny_{1}+my_{2}}{m+n} \).
Ha A(x1;y1) és B(x2;y2)=> \( \overrightarrow{OA} \)=\( \vec{a} \)(x1;y1), és \( \overrightarrow{OB} \) =\( \vec{b} \)(x2;y2), akkor \( \overrightarrow{OP}=\vec{p}\left(\frac{nx_{1}+mx_{2}}{m+n};\frac{ny_{1}+my_{2}}{m+n} \right) \)


Comments are closed, but trackbacks and pingbacks are open.