Differenciálhatóság és folytonosság kapcsolata.

Az f(x) = x² függvény mindenütt folytonos és minden pontban differenciálható.
Igaz-e, hogy minden folytonos függvény differenciálható?

Határozzuk meg az f(x) = |x| függvény deriváltját az x₀ = 0 pontban!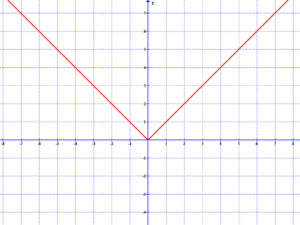

Képezzük a differenciahányadost az x₀=0 pontban! ​\( \frac{f(x)-f(x_0)}{x-x_0}=\frac{|x|-0}{x-0}=\frac{|x|}{x} \)​.

Képezzük a differenciahányados jobboldali határértékét: ​\( \lim_{ x^{+} \to 0}\frac{|x|-0}{x-0}=\lim_{ x^{+} \to 0}\frac{x-0}{x-0}=1; \; x>0 \)​.

Képezzük a differenciahányados baloldali határértékét:  ​\( \lim_{ x^{-} \to 0}\frac{|x|-0}{x-0}=\lim_{ x^{-} \to 0}\frac{-x-0}{x-0}=-1; \; x<0 \).

A jobb és a baloldali határértékek ugyan léteznek, de nem egyenlők egymással.
Így a differenciálhányados az x=x₀  pontban: ​\( d(x)=\frac{f(x)-f(x_0)}{x-x_0}=\frac{|x|}{x}=\left\{\begin{array}{} 1 & ha \; x>0 \\ -1 & ha \; x<0 \\ \end{array} \right\} \)​.

Tehát az f(x) = |x| függvénynek az x₀= 0 helyen nincs határértéke.

Ez azt jelenti, hogy az f(x) = |x| folytonos függvény nem differenciálható az x₀ = 0 pontban. Mindenhol máshol igen, de itt nem.

Ez egy példa arra, hogy nem minden folytonos függvény differenciálható.
Összhangban azzal, hogy az f(x) = |x| abszolút érték függvényhez az x₀ = 0 pontban nem lehet érintőt húzni („billegés”).
Ahol egy függvény egy adott pontban folytonos, de „csúcsa” van (a differenciahányadosok jobb és baloldali határértéke nem egyezik), ott nem differenciálható.

Viszont bizonyítható a következő tétel:

Ha az f(x) függvény differenciálható az x₀ pontban, akkor az f(x) függvény folytonos is az x₀ pontban.

Összefoglalva:

1. Tehát a függvény folytonossága a differenciálhatóság szükséges, de nem elégséges feltétele. Ha egy függvény egy adott pontban nem folytonos, akkor ebben a pontban nem differenciálható.
   Bolzano cseh matematikus készített egy olyan függvényt, amely minden pontban folytonos, de sehol sem differenciálható.
2. A differenciálhatóság a folytonosságnak elégséges, de nem szükséges feltétele.

Példa:

Ábrázoljuk a következő függvényt! ​\( f(x)=\frac{x^3+1.5x^2-1.5x-1}{x+2} \)​. x∈ℝ|x≠-2.

Ez a függvény egy harmadfokú és egy elsőfokú polinom hányadosa. Az osztás elvégzése (vagy a számláló szorzattá alakítása és egyszerűsítés után) a következő másodfokú függvényt kapjuk: f(x)=x²-0.5⋅x-0.5; x∈ℝ|x≠-2..

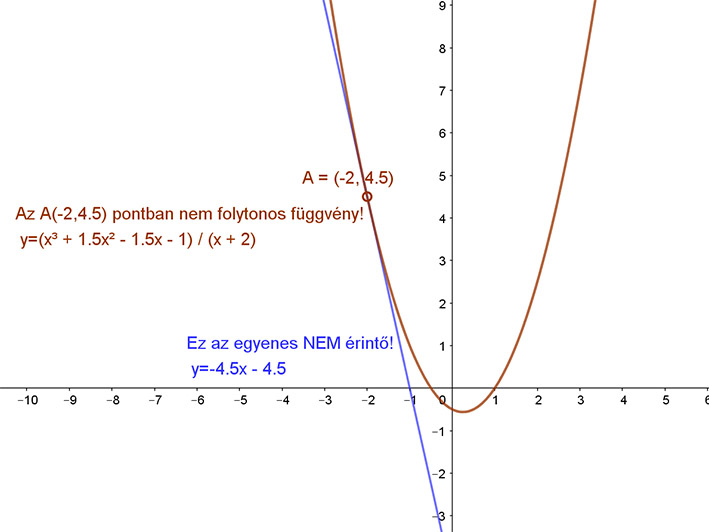
Ennek a függvénynek a képe egy olyan „lyukas” parabola, amely nincs értelmezve az x=-2 változó esetén. Az A=(2-,4.5) pont nem eleme a parabola grafikonjának.

Az y=-4.5⋅x-4.5 egyenes viszont áthalad ezen a ponton. „Úgy tűnik”, ez az egyenes érintője az eredeti ​\( f(x)=\frac{x^3+1.5x^2-1.5x-1}{x+2} \)​függvénynek. Igaz, hogy „hozzásimul”, de nem tudja érinteni ebben a pontban, mivel ez a pont nem pontja az eredeti függvénynek. Nincs hol érintenie!

Mivel az  ​\( f(x)=\frac{x^3+1.5x^2-1.5x-1}{x+2} \)  függvény nem folytonos az A=(2-,4.5) pontban, itt nem is differenciálható, ebben a pontban nem húzható hozzá érintő!

Megjegyzés: Az eredeti harmadfokú f(x) függvény szorzatalakban: ​\( f(x)=\frac{(x+2)·(x+0.5)·(x-1)}{x+2} \)​.

Az adott pontban a folytonosság szükséges feltétele differenciálhatóságnak, az adott pontbeli érintő létezésének.