Differenciahányados
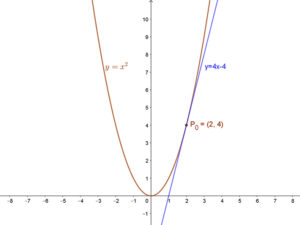Tekintsük az y = x2 egyenletű parabolát és jelöljük ki rajta a P0(2;4) pontot. Írjuk fel a parabolának ebbe a pontbajába húzható érintőjének egyenletét. Ehhez felhasználjuk, hogy az érintőnek egy közös pontja van a parabolával.
Mivel az egyenes egy pontját – a parabola P0(2;4) pontját – ismerjük, ezért a feladat az érintő meredekségének a meghatározása. Oldjuk meg a parabola egyenletének és az érintő paraméteres egyenletrendszerét!
Parabola egyenlete: y = x2. Az egyenes P0(2;4) ponton áthaladó „m” meredekségű egyenlete: y-4=m(x-2). Az egyenletrendszerből kapott másodfokú paraméteres egyenlet: x2=m(x-2)+4. Ennek egy megoldása akkor van, ha a diszkrimináns = 0.
Ez m = 4 esetén következik be, így az érintő egyenlete: y = 4x – 4.
Húzzunk most szelőket a Pi(x;x2) pontok és a P0(x0;y0) ponton át. Legyenek a Pi(x;x2) pontok: P1(-2;4); P2(-1.5;2,25); P3(-1;1); P4(-0,5; 0,25); P5(0; 0); P6(0,5; 0,25); P7(1; 1); P8(1,5; 2,25).
Számítsuk ki az egyes szelők meredekségét!
Foglaljuk eredményeinket táblázatba (x: a pontok első koordinátája, m: a szelő meredeksége):
|
x |
P1(-2;4) | P2(-1,5;2,25) | P3(-1;1) | P4(-0,5;0,250) | P5(-0;0) | P6(0,5;0,25) | P7(1;1) |
P8(1,5;2,251) |
|
m: |
0 | 0.5 | 1 | 1,5 | 2 | 2,5 | 3 |
3,5 |
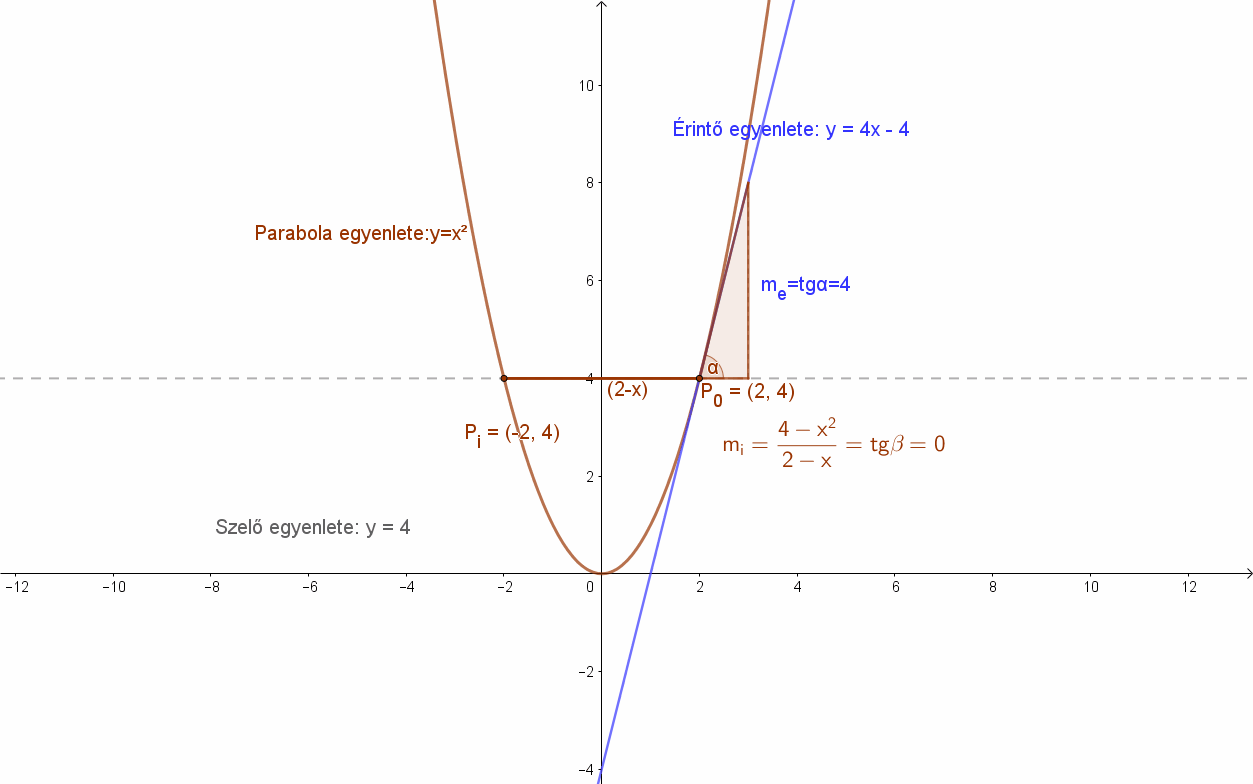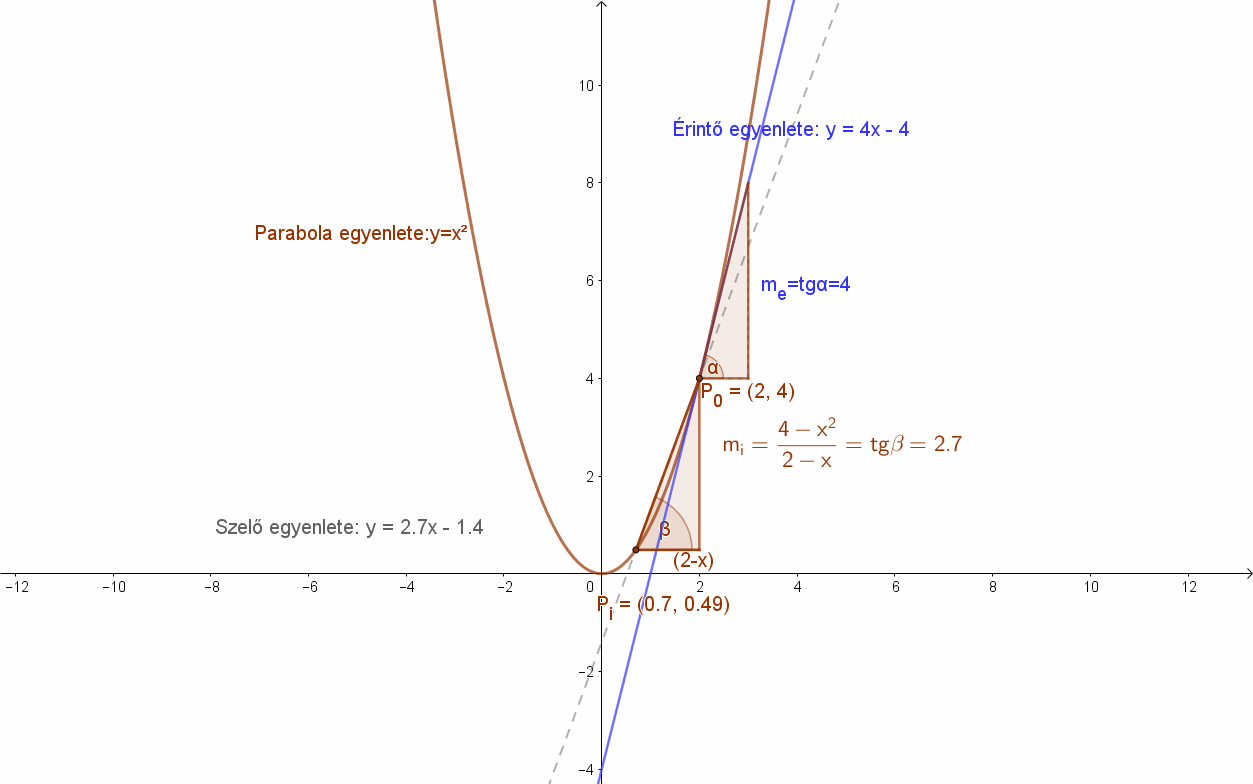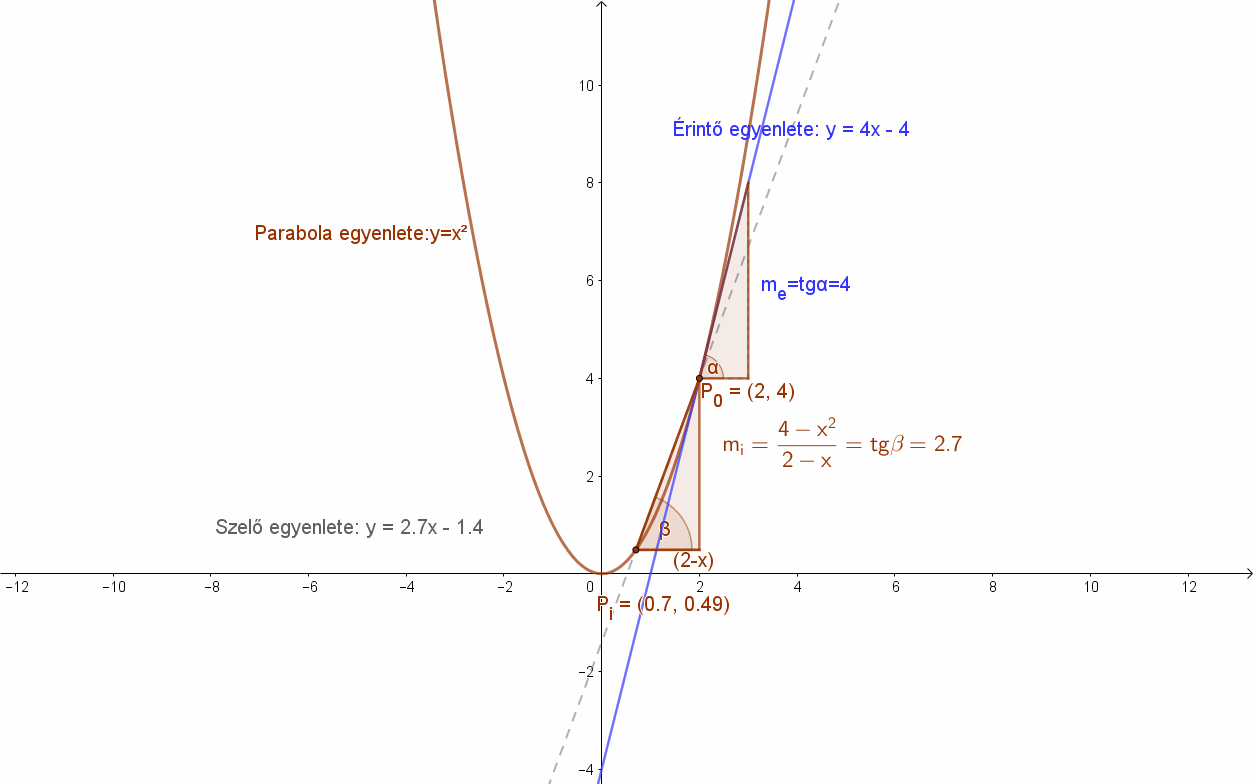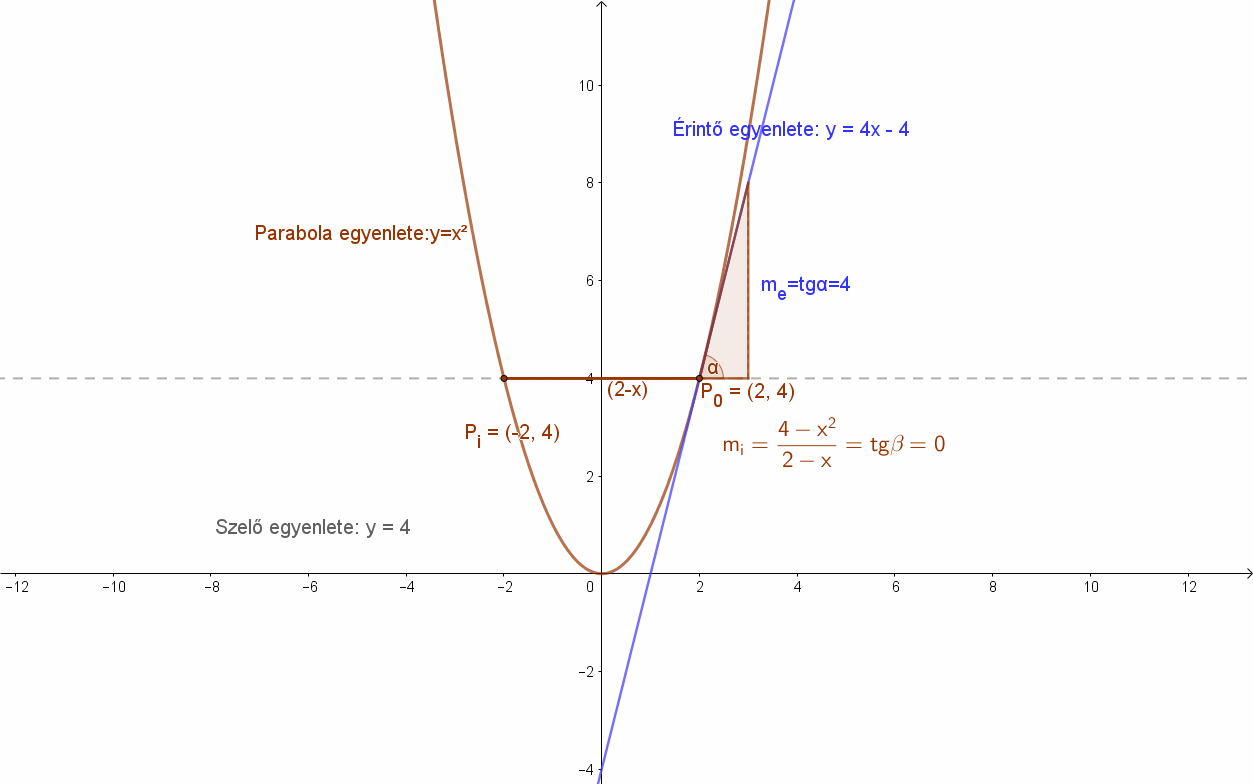
Ekkor a szelők meredeksége x függvényében: \( m(x)=\frac{4-x^{2}}{2-x} \) (differenciahányados).
Ennek a függvénynek van határértéke: \( \lim_{ x \to 2 }\frac{4-x^{2}}{2-x}=\lim_{ x \to 2 }\frac{(2-x)·(2+x)}{2-x}=\lim_{ x \to 2}(2+x)=4 \).
Valóban, az m =4 meredekségű egyenes a parabola P0(2;4) pontjába húzható érintő meredeksége.
Differenciahányados fogalma:
Az előző gondolatmenetünket általánosíthatjuk. Tekintsük az „f” függvény y = f(x) egyenletű grafikonján a P0(x0;y0) rögzített pontot. Az adott ponton átmenő, a görbe P(x; y=f(x)) pontját tartalmazó húregyenes (szelő) meredeksége: \( m(x)=\frac{f(x)-f(x_{0})}{x-x_{0}} \).
Definíció:
Legyen az f(x) függvény az x0 pont valamely környezetében értelmezve. Az adott f(x) függvény x0 pontjához tartozó \( g(x)=\frac{f(x)-f(x_{0})}{x-x_{0}} \) (x ≠ x0) függvényt az eredeti függvény adott x0 pontjához tartozó differenciahányadosának nevezzük.
Differenciálhányados fogalma:
Ha a differenciahányados függvénynek az x0 pontban van határértéke, akkor ezt a határértéket az „f” függvény x0 pontbeli differenciálhányadosának vagy rövidebben deriváltjának nevezzük.
Jelölés: \( f'(x); \; \frac{df}{dx}|x_{0} \).
A differenciálhányados fogalmának tisztázása többek között Weierstrass érdeme.
Ha a differenciálhatóság az „f” függvény értelmezési tartományának adott (a;b) – nyílt- intervallumában teljesül, akkor a függvényt az (a;b) –nyílt- intervallumban differenciálható függvénynek nevezzük.
Megjegyzés: Egy függvény adott pontjába húzható érintőjét (ha van ilyen) definiálhatjuk úgy is, mint az adott függvény adott pontjába húzott szelők határhelyzetét.
Egy fontos észrevétel:
Az a definíció, hogy az érintő a szelők határhelyzete általánosabb, mint a parabola esetében megfogalmazott érintő definíció.
Legyen adott egy harmadfokú függvény: f(x)=2x3+3x2-3x-2. Húzzunk szelőket a függvény Pi pontjain és P0(-1;2) pontján át. Azt fogjuk tapasztalni, hogy a szelők határhelyzete, a P0 pontba húzható érintőnek (y=-3x+1) nem egy hanem két közös pontja is van a függvénnyel. A P0(-1;2) ponton kívül az M(0.5;-2.5) pont is illeszkedik a függvény görbére és P0(-1;2) ponton áthaladó szelőre is. Az sem teljesül, hogy az érintő minden pontja külső pont lenne.
Érintő esetében a hangsúly a határhelyzeten, a „hozzásimuláson” van. Ez az értelmezés a kör és a parabola esetén is megállja a helyét.
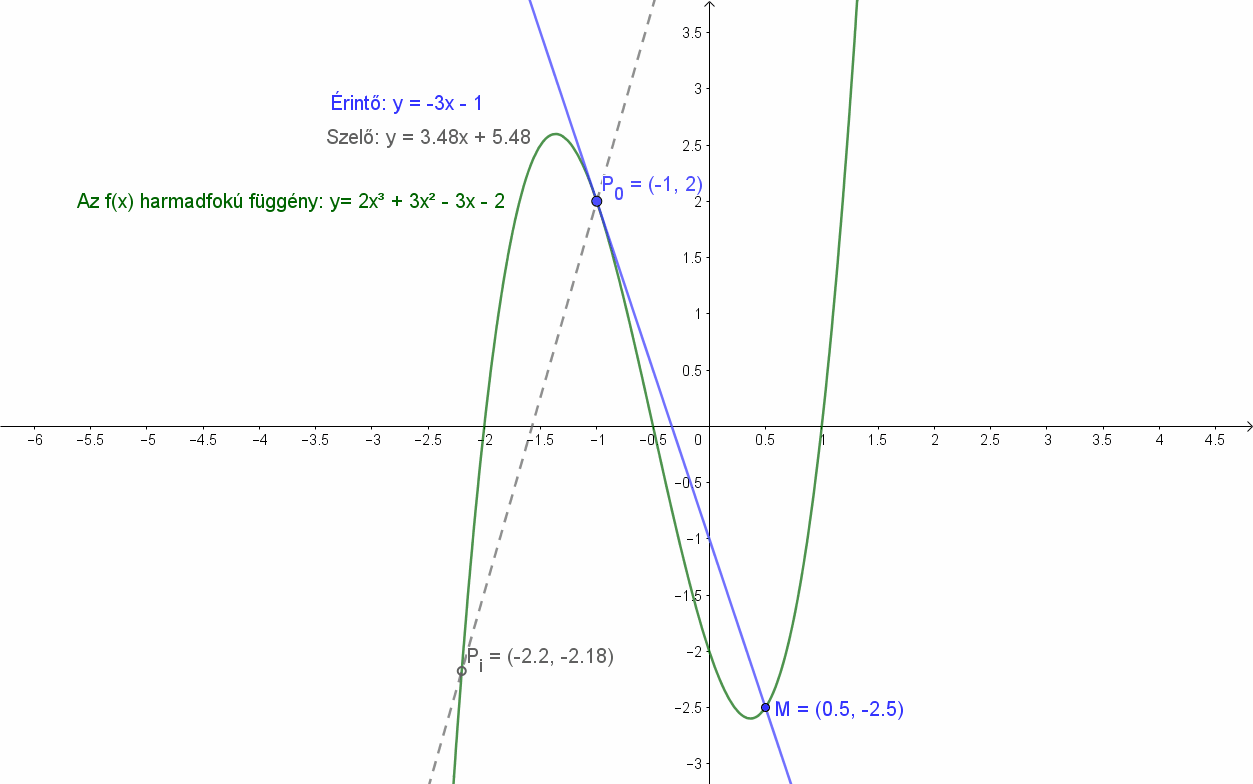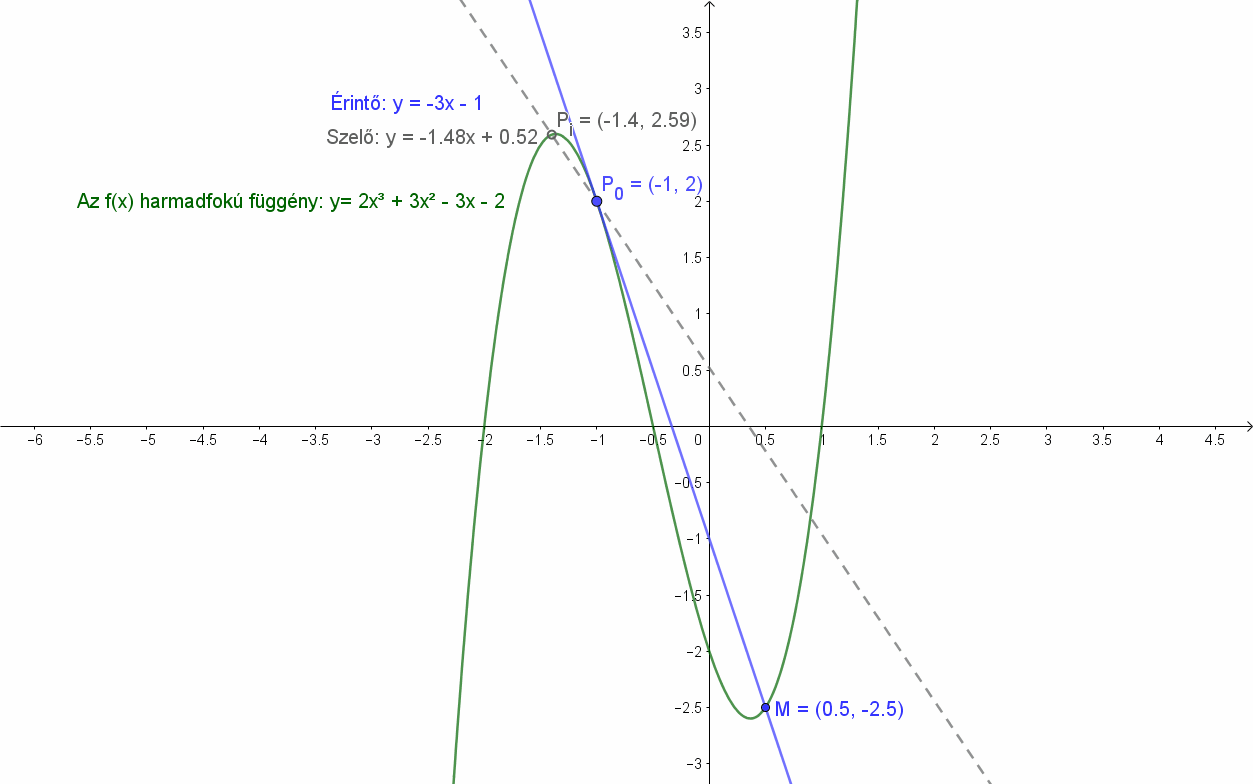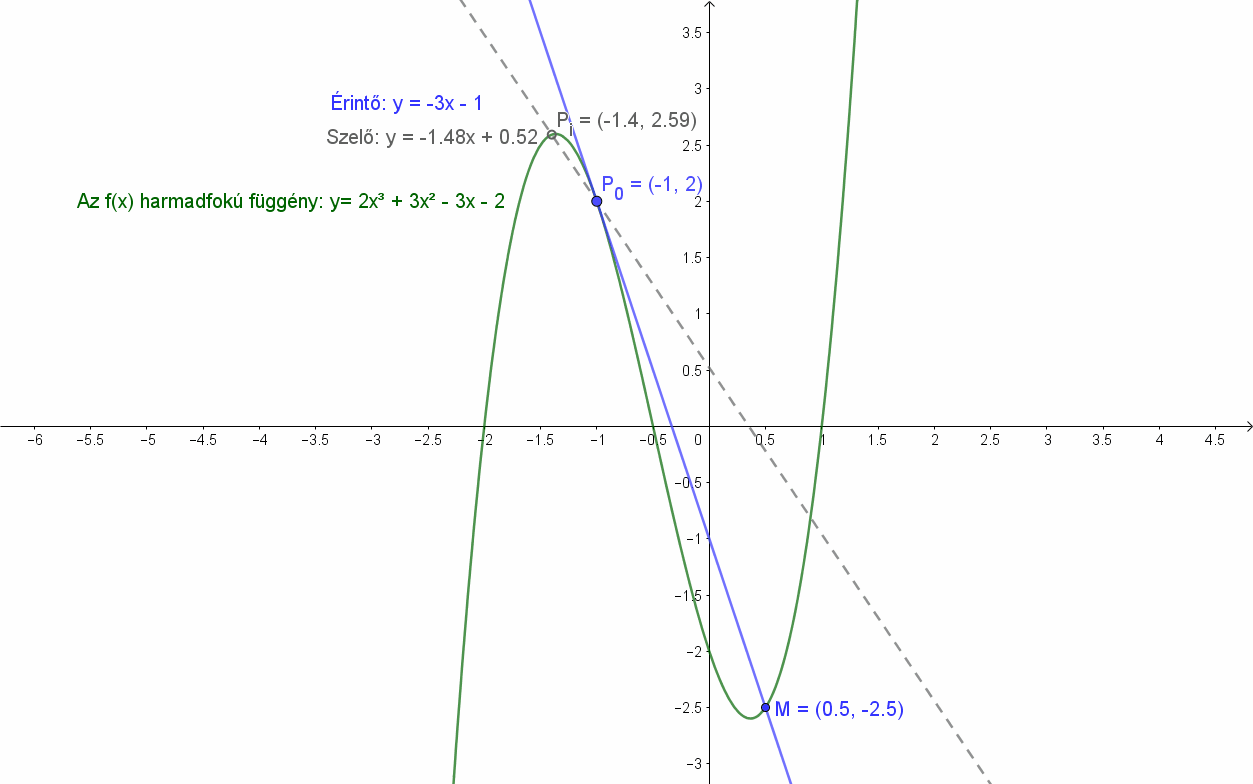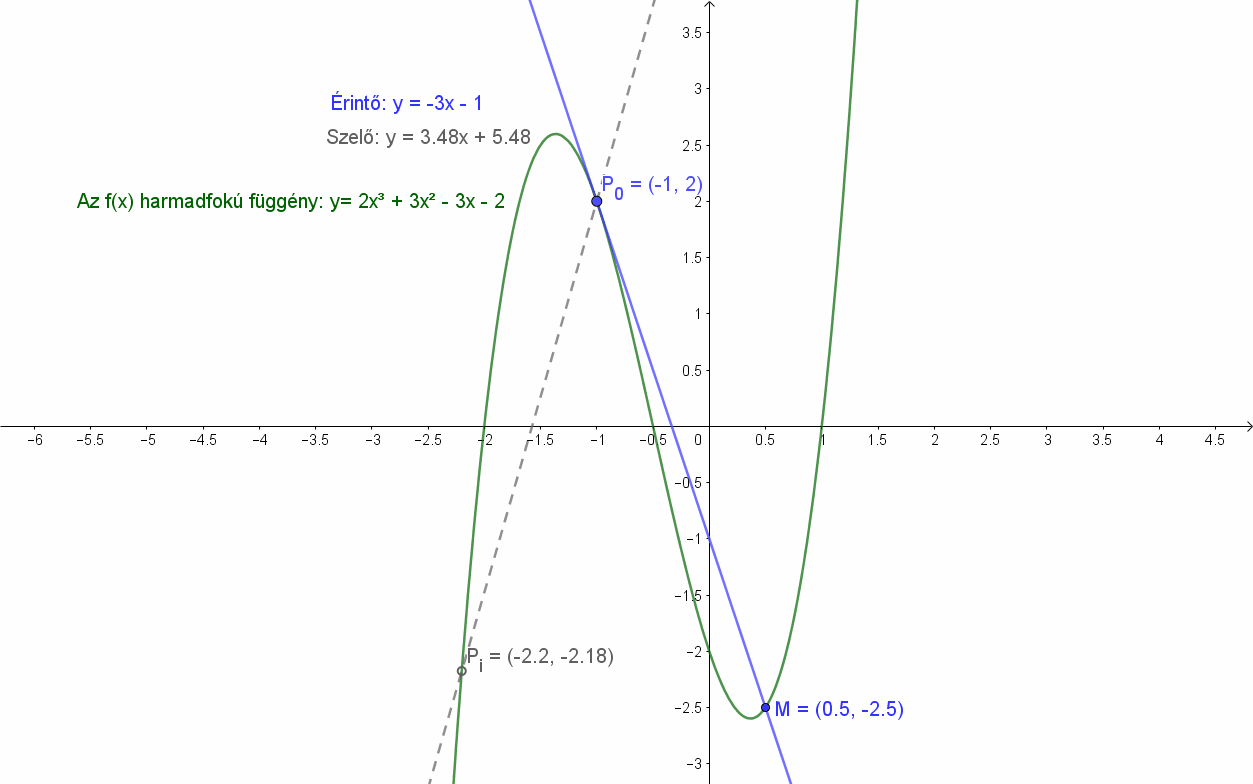
Általánosan: Egy adott „f” függvény differenciálhányadosa (ha van) megadja a függvénygörbe P(x0;f(x0)) pontjában a görbéhez húzható érintő iránytangensét (meredekségét).
Deriváltfüggvény fogalma:
Azt a függvényt, amelyik megadja, hogy a változó egyes értékeihez milyen differenciálhányados (derivált) tartozik, azt az f(x) függvény deriváltfüggvényének vagy röviden deriváltjának nevezzük és az f’(x) vagy \( \frac{df}{dx} \)a szimbólummal jelöljük.
A differenciálhatóság alapvetően egy adott pontra (x0) vonatkozik. Ha egy adott függvény az értelmezési tartományának nyílt intervallumának minden pontjában differenciálható, akkor a függvényt a nyílt intervallumon differenciálható függvénynek mondjuk.
Az f függvény derivált függvényének (differenciálhányados-függvényének) nevezzük azt az f’ függvényt, amely értelmezve van azokon az x0 helyeken, ahol az f függvény differenciálható és ott az értéke f’(x0).
Feladat
Igazoljuk, hogy az f: R→R, f(x) = x2 függvény mindenütt differenciálható!
Bizonyítás:
A tetszőleges,de rögzített x0 ponthoz tartozó differenciahányados: \( \frac{f(x)-f(x_0)}{x-x_0}=\frac{x^2-x^2_0}{x-x_0}=\frac{(x-x_0)·(x+x_0)}{x-x_0}=x+x_0 \).
Képezzük a differenciahányados határértékét az x0 pontban! \( \lim_{ x \to x_0 }(x+x_0)=2·x_0 \).
Mivel x0 az értelmezési tartomány tetszőleges eleme, ezért az f(x) = x2 függvény mindenütt differenciálható és tetszőleges x pontban a differenciálhányados : 2⋅x.
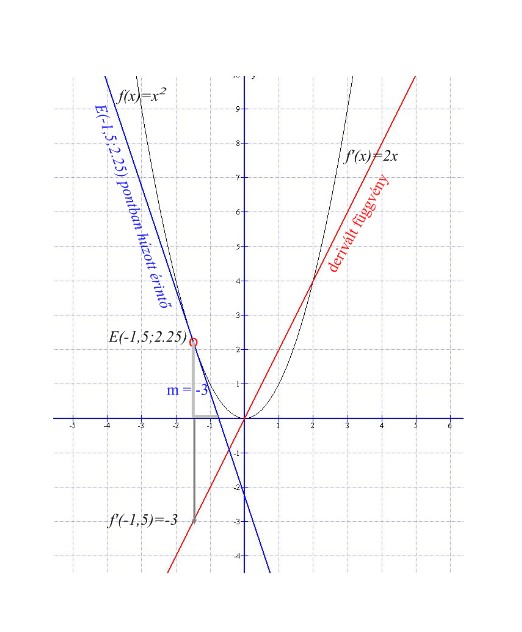
Az f(x) = x2 függvény deriváltfüggvénye f’(x)= 2⋅x. Az f’(x)=2⋅x függvény adott pontban vett függvényértéke értéke megadja az f(x)=x2 függvényhez az adott pontban húzható érintő meredekségét (iránytangensét).
Például: f’(-1,5)=-3 azt jelenti, hogy az f(x) = x2 függvényhez az x = -1.5 pontban húzott érintő meredeksége -3.
Comments are closed, but trackbacks and pingbacks are open.