Csonkakúp térfogata

Ennek a tételnek a bizonyítása a csonkagúla térfogatának a levezetésének menetét követi.

A csonkakúp térfogatának meghatározásánál a következőket használjuk fel: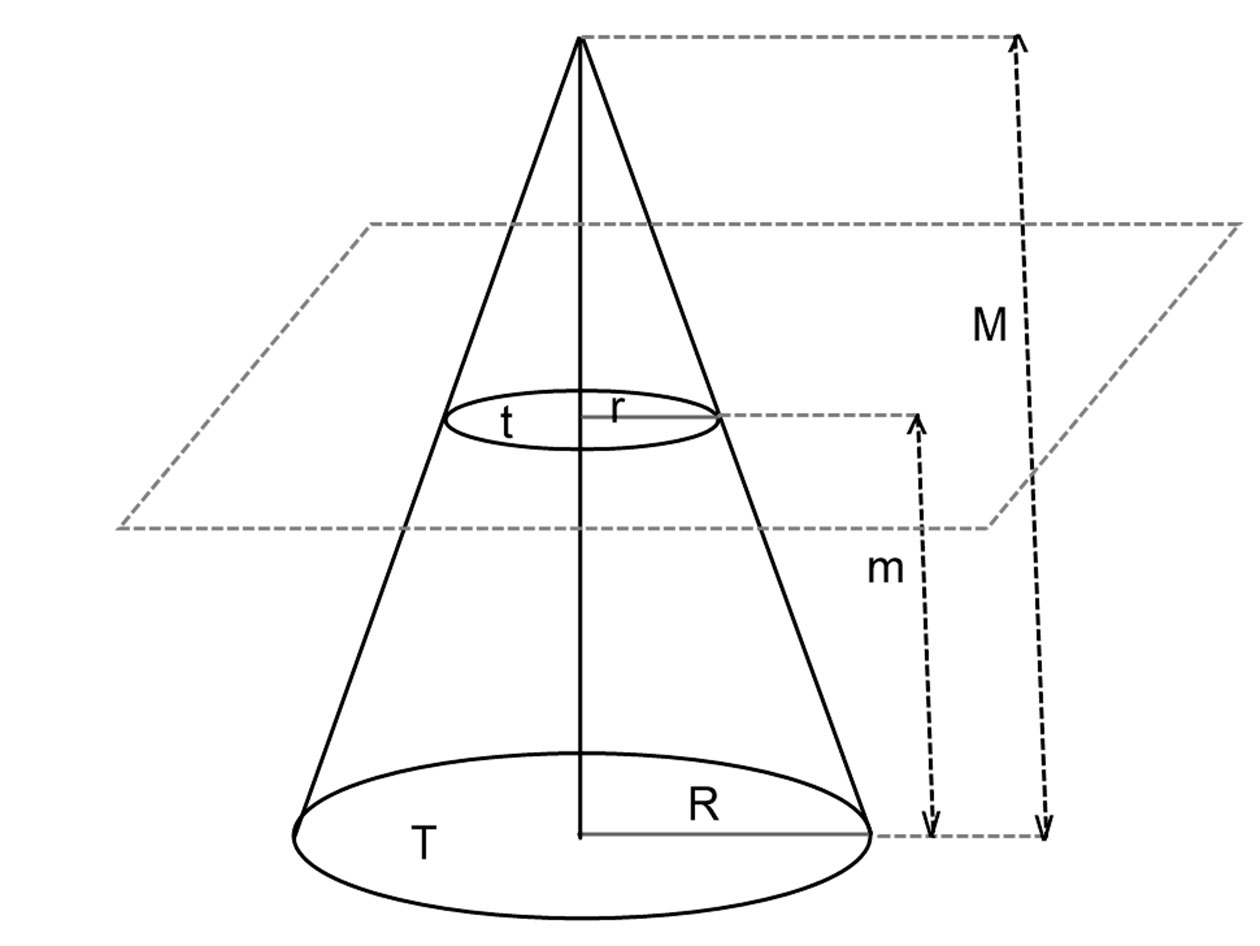

• A teljes, nem csonka kúp térfogata: ​\( V_{kúp}=\frac{t_{kör}·M_{kúp}}{3} \)​, azaz ​\( V_{kúp}=\frac{r^2· π ·M}{3} \)​.
• A középpontos hasonlóságot.

A csonka kúp térfogatának meghatározásánál egy teljes kúpból indulunk ki. Ennek felső részéből levágunk egy kisebb, az eredetihez középpontosan hasonló kúpot.

Jelölések:

Csonka kúp: R alapkör sugara,  r: fedőkör sugara, m csonka kúp magassága, V térfogat.
Eredeti teljes kúp: R kör sugara, M kúp magasság, V₁ térfogat, ahol: ​\( V_{1}=\frac{R^2· π ·M}{3} \)​.

Hozzá középpontosan hasonló, levágott kiskúp: r kör sugara, M-m kúp magasság, V₂ térfogat, ahol: ​\( V_{2}=\frac{R^2· π ·(M-m)}{3} \)​.

Mivel a levágott kis kúp és az eredeti teljes kúp középpontosan hasonló, ahol a hasonlóság középpontja az eredeti kúp csúcsa, és jelöljük a hasonlóság arányát λ-val.

Felhasználva a hasonló sokszögek területeire és a hasonló testek térfogataira szóló tételt:

​\( λ=\frac{m_{1}}{m_{2}} \; és \; λ^2=\frac{T}{t} \; valamint \; λ^3=\frac{V_{1}}{V_{2}} \) azaz

​\( λ=\frac{R}{r}, \; λ=\frac{M}{M-m} \; és \; λ^2=\frac{R^2}{r^2} \; valamint \; λ^3=\frac{V_{1}}{V_{2}} \)​, azaz R=λ⋅r, M=λ⋅(M-m) és V₁=λ³⋅V₂.

V=V₁-V₂ egyenlőségből
V=λ³⋅V₂-V₂. Itt V₂-t kiemelve: V=V₂(λ³-1).
(λ³-1)-t szorzat alakba írva: V=V₂(λ-1)(λ²+λ+1), de V₂-t helyettesítve: V=r²π(M-m) (λ-1)(λ²+λ+1)/3 adódik.
Itt (λ-1) tényezőt (M-m)-el, a (λ²+λ+1) tényezőt pedig r²– tel szorozva: V=π [(λ(M-m)-(M-m)]( λ²r²+λr²+ r²)/3.

Felhasználva, hogy λ⋅(M-m)=M és, λr=R miatt λ⋅r²=R⋅r kapjuk hogy V=π [(M-(M-m))](R²+Rr+r²)/3 alakot kapjuk. Ebből:

​\( V=\frac{m· π ·(R^2+R·r+r^2)}{3} \)​.

És ezt kellett bizonyítani.