Ennek a tételnek a bizonyítása a csonka kúp térfogatának a levezetésének menetét követi.
A csonka gúla térfogatának meghatározásánál a következőket használjuk fel:
- A teljes, nem csonka gúla térfogata: \( V_{gúla}=\frac{T_{alap}·m_{gúla}}{3} \) .
- A középpontos hasonlóságot.
A csonka gúla térfogatának meghatározásánál egy teljes gúlából indulunk ki. Ennek felső részéből levágunk egy kisebb, az eredetihez középpontosan hasonló gúlát.
Jelölések:
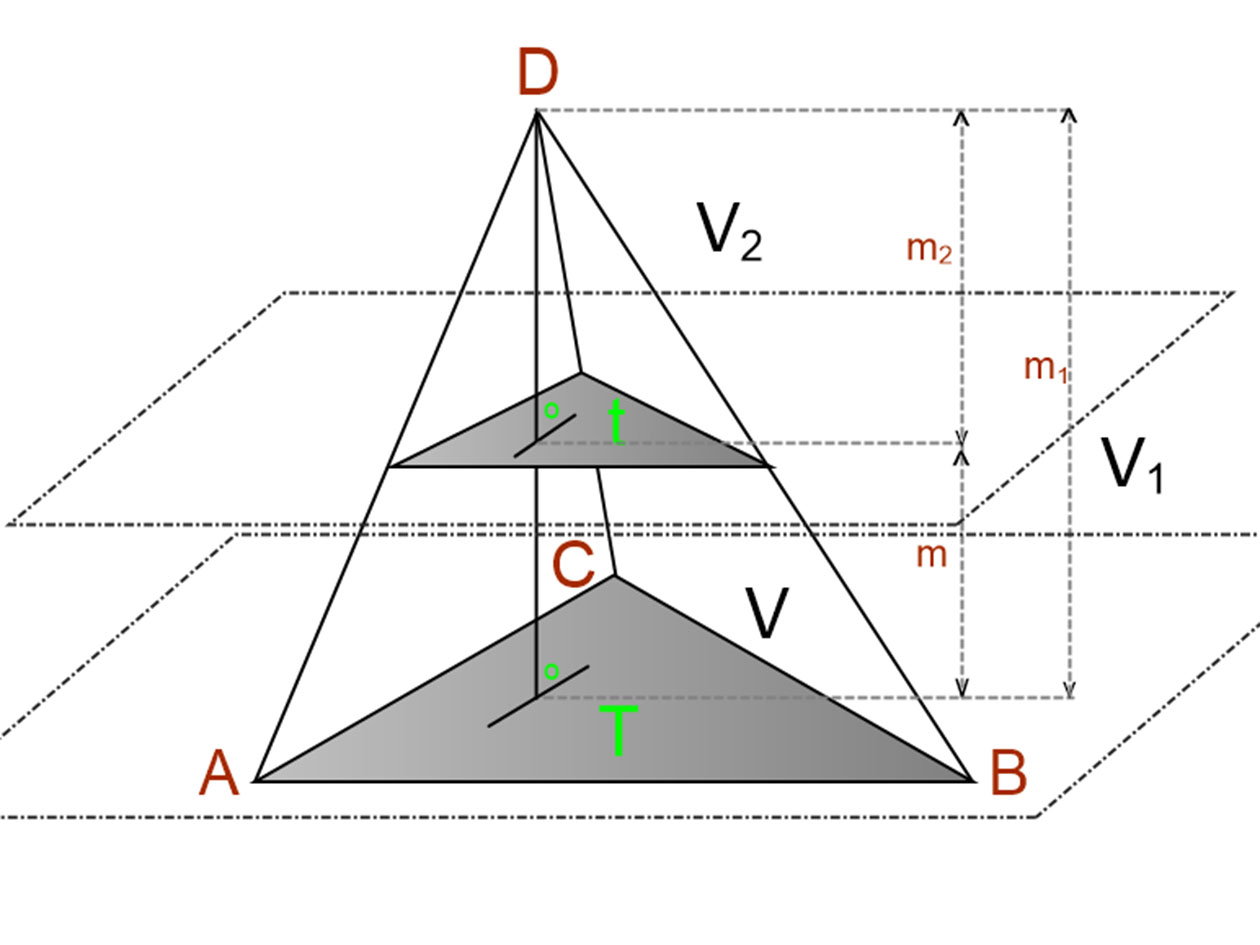 Eredeti teljes gúla:
Eredeti teljes gúla:
T: alapterület, m1 gúla magasság, V1 térfogat, ahol \( V_{1}=\frac{T·m_{1}}{3} \).
Hozzá középpontosan hasonló, levágott kisgúla:
t: alapterület, m2 gúla magasság, V2 térfogat, ahol \( V_{2}=\frac{t·m_{2}}{3} \).
Csonka gúla:
T alaplap területe, t: fedőlap területe, m csonka gúla magassága, V térfogat. Itt
m=m1–m2 és V=V1–V2.
Mivel a levágott kis gúla és az eredeti teljes gúla középpontosan hasonló, ahol a hasonlóság középpontja az eredeti gúla csúcsa, és jelöljük a hasonlóság arányát λl-val.
Felhasználva a hasonló sokszögek területeire és a hasonló gúlák térfogataira szóló tételt: \( λ=\frac{m_{1}}{m_{2}} \; és \; λ^2=\frac{T}{t} \; valamint \; λ^3=\frac{V_{1}}{V_{2}} \).
Átrendezve: m1 = λ⋅m2, és T=λ2⋅t, valamint V1=λ3V2.
V=V1-V2 egyenlőségből V=λ3V2-V2.
Itt V2-t kiemelve: V=V2(λ3-1).
(λ3-1)-t szorzat alakba írva: V= V2(λ-1)(λ2+λ+1), de V2-t helyettesítve: V= t⋅m2(λ-1)( λ2+λ+1)/3 adódik.
Itt (λ-1) tényezőt m2-vel, a (λ2+λ+1) tényezőt pedig t-vel szorozva:
V= (λm2-m2)( λ2t+λt+t)/3.
Itt felhasználva, hogy λm22= m1 és, λ2t=T,
V= ( m1– m2)(T+λt+t)/3 alakot kapjuk.
T= λ2 t egyenlőségből Tt=λ2 t2, ezért: \( λ·t=\sqrt{T·t} \).
A csonka gúla térfogata tehát: \( V=\frac{m·(T+\sqrt{T·t}+t)}{3} \).
A kb. Kr.e. 1700-ból származó un. moszkvai papirusz tanúsága szerint az ókorban az egyiptomiak már a fenti képlet szerint számolták a négyzet alapú csonka gúla térfogatát!
|
|
|




Comments are closed, but trackbacks and pingbacks are open.