Az inverz függvény

Az inverz függvény:

Legyen adott egy olyan f(x) függvény, amely kölcsönösen egyértelmű megfeleltetést létesít a D_f értelmezési tartomány és az R_f értékkészlet elemei között.

Definiáljuk a következő függvényt: f: (R\R^–)→ R, f(x)=x². Ennek függvénynek az értelmezési tartománya most a nemnegatív valós számok halmaza. Ez kölcsönösen egyértelmű hozzárendelést jelent az értelmezési tartomány és az értékkészlet elemei között. A kölcsönösen egyértelmű megfeleltetésből következik, hogy az értékkészlet minden eleméhez csak egy elem tartozik az értelmezési tartományból.

Például: az f(x)=x² hozzárendelés a 3-hoz a 9-t rendeli, és most ezen az értelmezési tartományon a 9 érték csak a 3 helyettesítési értéke, azaz f(3)=3²=9.

A kölcsönösen egyértelmű hozzárendelés miatt azonban a kapcsolat meg is fordítható.

Az új függvény értelmezési tartománya az előző függvény értékkészlete, és értékkészlete az eredeti függvény értelmezési tartománya.

Így most a 9-hez rendeljük a 3-t, a 4-hez a 2-t stb. Ez pedig a g(x)=​\( \sqrt{x} \) ​függvény. A  g(x)=​\( \sqrt{x} \)​ és az f(x)=x²  függvény egymás inverzei.

Definíció:

Az f függvénynek a g függvény az inverze, ha az f függvény értelmezési tartományának minden x elemére teljesül, hogy az f(x) függvényérték eleme a g függvény értelmezési tartományának és f(g(x)=g(f(x)=x
Az f(x) függvény inverzének jelölése: f^-1(x)

Az inverz függvények grafikonjai szimmetrikusak az y=x egyenesre.

Például az f(x)=x² és g(x)=​\( \sqrt{x} \)​függvények (és x≥0)  esetén ​\( f(g(x))=(\sqrt{x})^2=x \)​.  Azaz ​\( f(g(x))=(\sqrt{x})^2=x \)​ és  ​\( g(f(x))=\sqrt{x^2}=x \)​

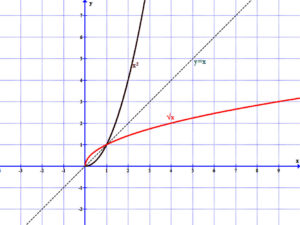
Az alábbi ábrákon olyan közismert függvényeket találunk, amelyek egymás inverzei:

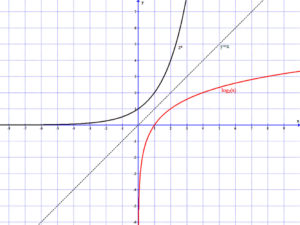
Az f: (R\R–)→ R, f(x)=x2 és a  g(x)=​\( \sqrt{x} \)​​ függvények grafikonjai egy koordináta-rendszerben	Az f(x)=2x és g(x)=log2(x) függvények grafikonjai egy koordináta-rendszerben

További példa:

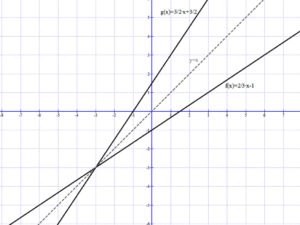
Legyen ​\( f(x)=\frac{2}{3}x-1 \)​ és ​\( g(x)=\frac{3}{2}x+\frac{3}{2} \)​. Ekkor: ​\( f(g(x))=\frac{2}{3}·\left( \frac{3}{2}x+\frac{3}{2}\right)-1 \)​. Könnyű belátni, hogy ​\( f(g(x))=\frac{2}{3}·\left( \frac{3}{2}x+\frac{3}{2}\right)-1=x \)​.

És ugyan így : ​\( g(f(x))=\frac{3}{2}·\left( \frac{2}{3}x-1\right) +\frac{3}{2} \)​. Itt is könnyű belátni, hogy ​\( g(f(x))=\frac{3}{2}·\left( \frac{2}{3}x-1\right) +\frac{3}{2}=x \)​.

Tehát az  ​\( f(x)=\frac{2}{3}x-1 \)​ és a ​\( g(x)=\frac{3}{2}x+\frac{3}{2} \)​egymás inverzei.

Hogyan invertálhatunk egy függvényt?

Egyszerűbb esetekben egy függvény invertálásakor a függvény hozzárendelési szabályából indulunk el.

A függvény hozzárendelési szabályának egyenletében (ha van ilyen) formálisan felcseréljük az „x” és „y” változókat. Majd a felcserélés után kapott egyenletet y-ra rendezzük.