Bevezető példa:
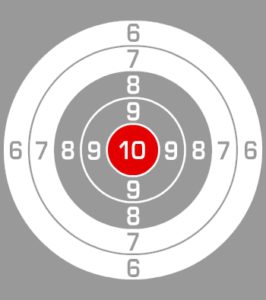Egy célba lövő egy 50 cm oldalú négyzet alakú táblára lő. Feltételezzük, hogy lövései egyenlő eséllyel érik el a céltábla bármely pontját. Mi a valószínűsége annak, hogy a tábla közepén lévő 10 cm átmérőjű körbe talál?
(Készüljünk az érettségire matematikából közép-, emelt szinten. (MK-2947-3, 284. oldal)
Megoldás:
Az nyilvánvaló, hogy ebben az esetben a valószínűségszámítás klasszikus (kombinatorikus) modellje nem alkalmazható. Az eseménytér (a céltábla pontjai) végtelen számú elemi eseményből áll.
Az természetesnek tűnik, hogy ha egy céltáblára egy adott távolságból lövünk, akkor a legkisebb az esélye (valószínűsége) annak, hogy a céltábla közepébe, a legkisebb sugarú körbe fogunk találni. Másként fogalmazva: a valószínűség a területtel arányos.
A négyzet területe: 502=2500 cm2. A 10 cm átmérőjű belő kör területe: 102⋅π≈78,54.
A két terület aránya≈78,54/2500≈0,0314. Százalékban kifejezve: 3,14%.
Defínició:
Ha a „H” eseménytér mérhető (például van hossza, területe vagy térfogata) és eseményei mérhetők és valószínűségük egyenesen arányos a mértékükkel, akkor ezt az eseményteret az eseményeivel és a közöttük értelmezett műveletekkel (összeadás, kivonás, szorzás, komplementer) együtt geometriai valószínűségi mezőnek nevezzük.
Tétel:
Ha „H” a geometriai valószínűségi mező eseménytere, a rajta értelmezett mérték (például hossz, terület vagy térfogat) M és az „A” eseménynek megfelelő részalakzat mértéke m, akkor az A esemény valószínűsége:
\[ \( P(A)=\frac{az \; “A” \; eseménynek \; megfelelő \; részhalmaz \; mértéke}{a \; kísérlettel \; kapcsolatos \; teljes \; alakzat \; mértéke}=\frac{m}{M} \) \]
A geometriai valószínűség esetén több fontos megjegyzést kell tenni.
Vegyük példának a céltáblára lövést. Elemi esemény, ha a céltábla egy pontját eltaláljuk. Tehát ez az eseménytér végtelen. Biztos eseménynek tételezzük fel, hogy a lövés eltalálja a céltáblát (azaz 1 valószínűséggel érkezik a céltáblára), viszont 0 valószínűsége, hogy eltalálunk egy adott pontot, mivel egy pont mértéke: m=0.
Ez tehát egy olyan esemény, amelynek 0 a valószínűsége, mégsem lehetetlen esemény.
Feladat:
Egy távbeszélőállomás és a központ közötti vezeték hossza 450 méter. Mi annak a valószínűsége, hogy az első hiba a vezetéknek a központtól 180 méternél távolabbi helyén lép fel, feltételezve, hogy a vezeték mentén bárhol azonos a meghibásodás veszélye?
Solt György: Valószínűségszámítás 100. oldal
Megoldás:
Az „A” esemény mértéke: m=450-180= 270 méter. Így a keresett valószínűség: P(A)=\frac{270}{450}=\frac{3}{5}=0,6. Százalékban: 60%.
Feladat:
Egy 10 egységnyi oldalú négyzet alakú táblában elhelyezett kör alakú céltáblára véletlenszerűen érkeznek pontszerű lövések. A körök sugarai: 1; 2; 3; 4 és 5 egység. Ha a legnagyobb körön kívül esik a találat, akkor az 0 pontot ér. Mennyi a valószínűsége, hogy a legnagyobb sugarú, külső körbe találunk?
Megoldás:
Számítsuk ki annak a valószínűségét, hogy a legkülső körbe érkezik a lövés! Jelöljük ezt az eseményt A5-tel. A négyzet területe 100 egység2, míg a legkülső körgyűrű területe: m=25⋅π-16⋅π=9⋅π
Így a külső körbe érkező találat valószínűsége: \( P(A_{5})=\frac{9 π }{100}≈0,283 \). Százalékban kifejezve: 28,3%.
Ehhez hasonlóan számítható ki a többi körbe eső találat valószínűsége.
Comments are closed, but trackbacks and pingbacks are open.