A koordináta-rendszerben adott két pont távolságának a meghatározása

Tétel:

Ha adott a koordináta-rendszerben az A(a₁;a₂) és B(b₁;b₂) pontok, akkor a két pont távolsága egyenlő a két pont megfelelő koordináták különbségeinek négyzetösszegéből vont négyzetgyökével. ​\( AB=d=\sqrt{(b_{1}-a_{1})^2+(b_{2}-a_{2})^2} \)​

Bizonyítás:

Két pont távolsága egyenlő a két pont által meghatározott vektor abszolút értékével. A két pont által meghatározott vektor a két pont helyvektorának különbsége.

Az A pontból a B pontba mutató vektort jelöljük ​\( \vec{v} \)​-vel a mellékelt ábra szerint:
​​\( \vec{v}=\vec{b}-\vec{a} \)​=>​\( \vec{v} \)​(b₁-a₁;b₂-a₂).

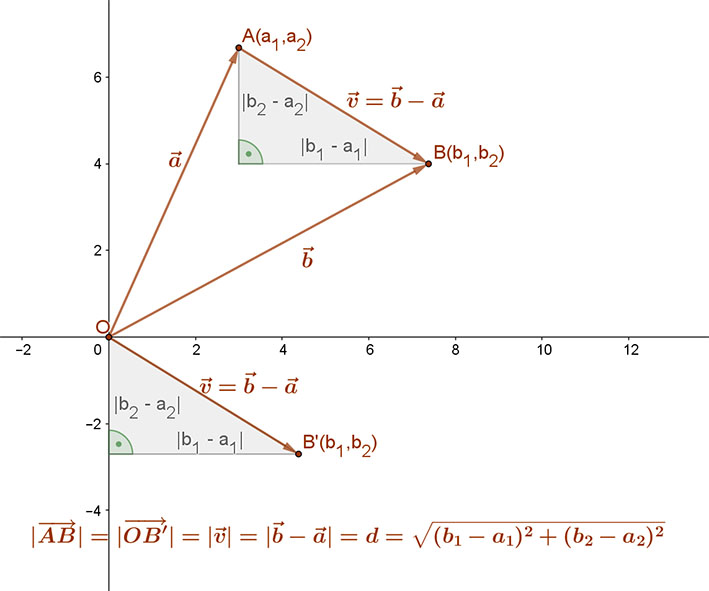
A ​\( \vec{v} \)​ vektor hossza a vektorral és koordinátáival képzett derékszögű háromszögből Pitagorasz tételével számítható, hiszen a derékszögű háromszög befogói a pontok koordinátái különbségének abszolút értéke.
Felírva tehát a Pitagorasz tételét:
d²=(b₁-a₁)²+(b₂-a₂)².

Ebből négyzetgyökvonással kapjuk az állítást:

 ​\( d=\sqrt{(b_{1}-a_{1})^2+(b_{2}-a_{2})^2} \)​