Tétel:
A háromszög három belső szögfelezője egy pontban metszi egymást.
Bizonyítás:
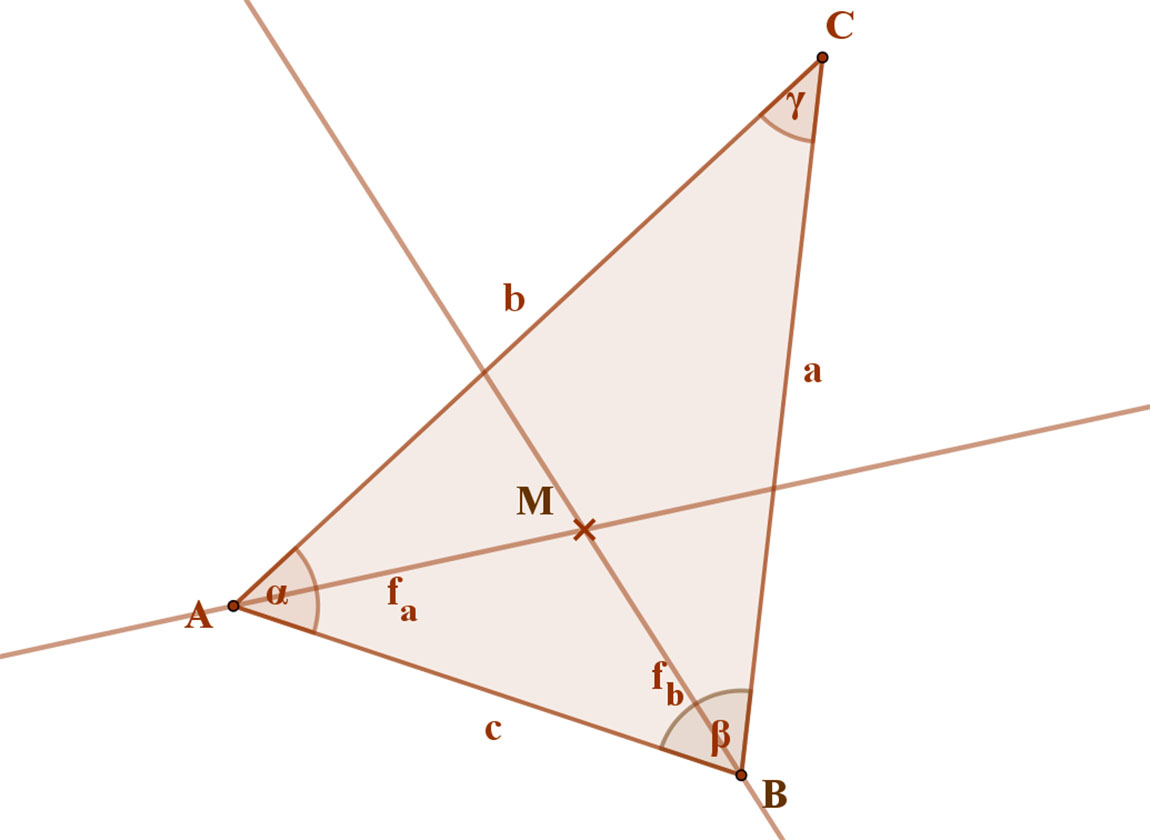 Tudjuk, hogy a szögfelező félegyenes azoknak a pontoknak a halmaza, amelyek egyenlő távolságra vannak a szög száraitól.
Tudjuk, hogy a szögfelező félegyenes azoknak a pontoknak a halmaza, amelyek egyenlő távolságra vannak a szög száraitól.
Tekintsük a mellékelt ABC háromszöget ahol meghúztuk az A csúcsból induló fa és a B csúcsból induló fb belső szögfelezőt. Az fa szögfelező minden pontja egyenlő távol van a háromszög AC és AB oldalaitól. Az fb szögfelező minden pontja egyenlő távol van a háromszög AB és BC oldalaitól. A két szögfelező metszi egymást egy M pontban.
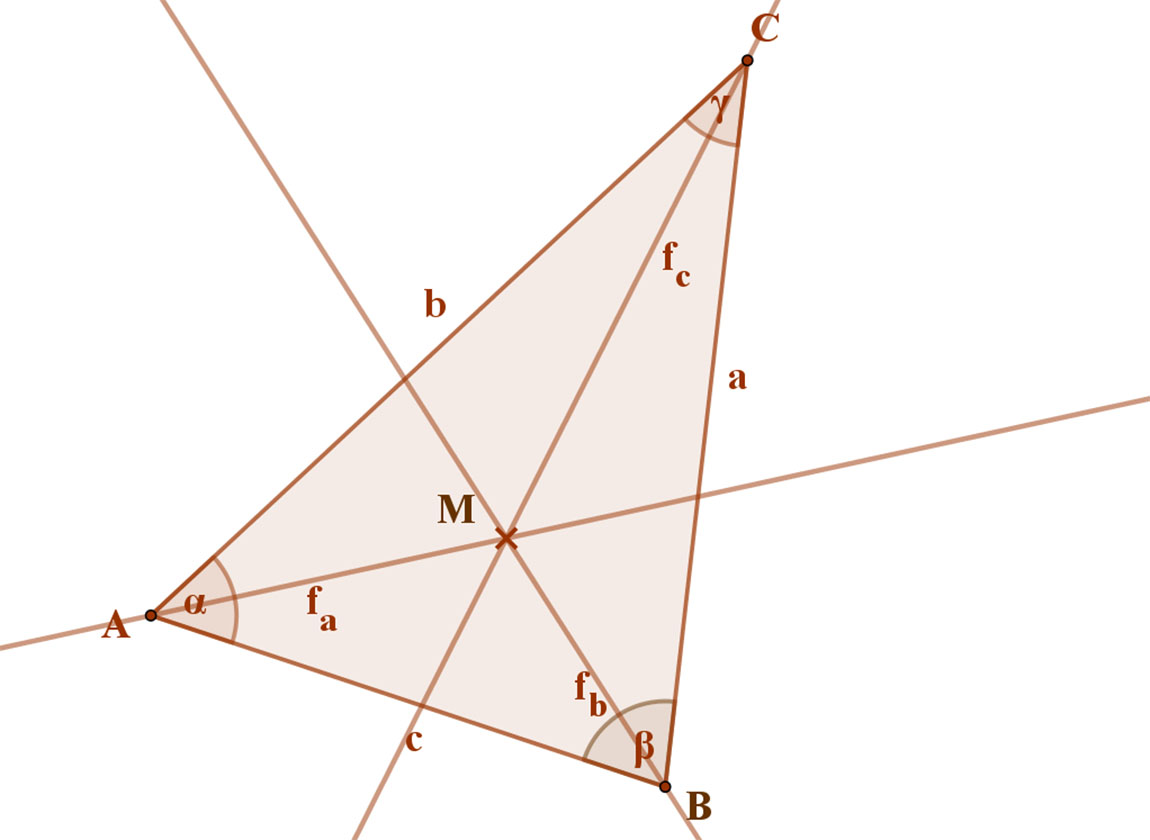 Mivel M pont rajta van az fa szögfelezőn, ezért egyenlő távol van AB és AC oldalaktól, de rajta van fb szögfelezőn is, tehát egyenlő távol van AB és BC oldalaktól is.
Mivel M pont rajta van az fa szögfelezőn, ezért egyenlő távol van AB és AC oldalaktól, de rajta van fb szögfelezőn is, tehát egyenlő távol van AB és BC oldalaktól is.
Ez azt jelenti, hogy az M pont egyenlő távol van a háromszög mindhárom oldalától, ezért az M pontnak illeszkednie kell a C csúcsból induló fc szögfelezőre.
Így beláttuk, hogy a háromszög belső szögfelezői egy pontban metszik egymást.
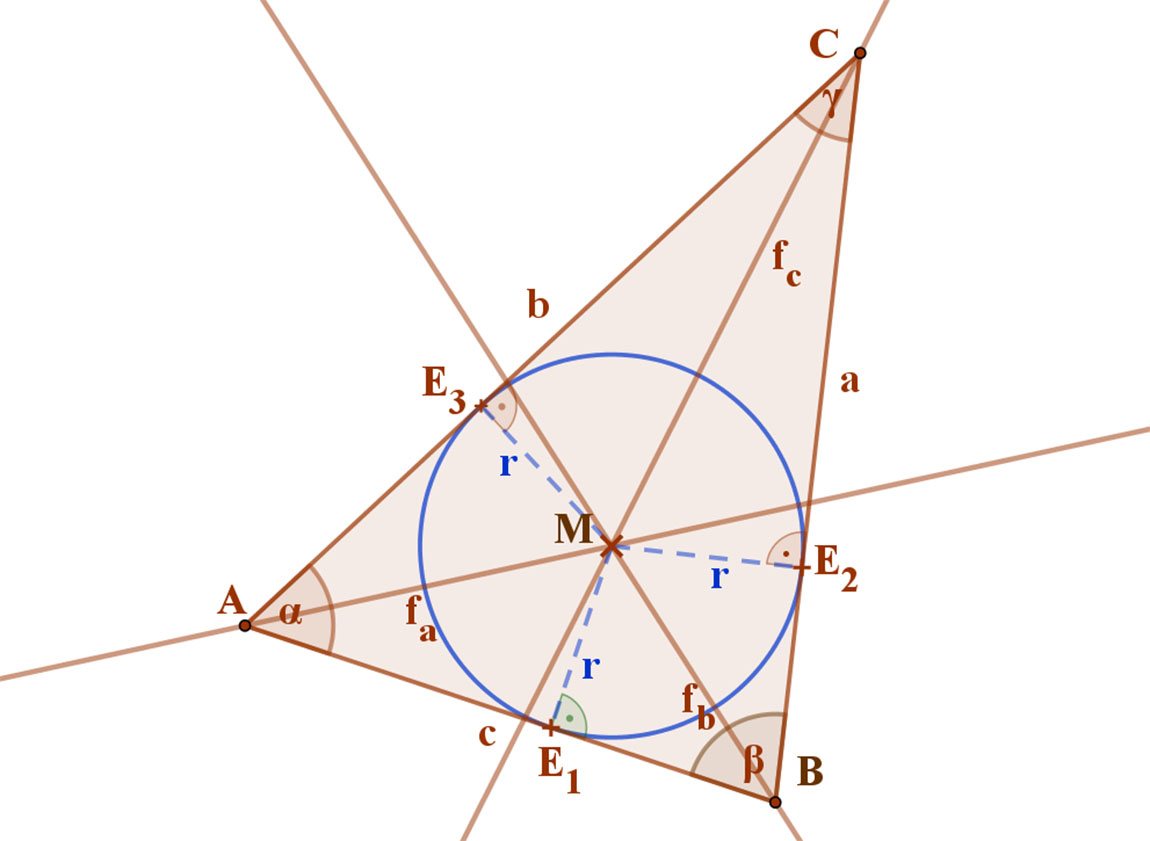 Ez a pont a háromszög oldalait érintő beírt kör középpontja. A beírt kör sugarát megkapjuk, ha a szögfelezők metszéspontjából merőlegest bocsátunk a háromszög oldalaira.
Ez a pont a háromszög oldalait érintő beírt kör középpontja. A beírt kör sugarát megkapjuk, ha a szögfelezők metszéspontjából merőlegest bocsátunk a háromszög oldalaira.
Alkalmazás, következmény:
1. Az „a” „b” befogójú és a „c” átfogójú derékszögű háromszög esetén igaz a következő összefüggés:
c=a-r+b-r= a+b-2⋅r
2. A háromszög területe (T), kerülete (K) valamint a háromszög beírt köre sugara (rb) hossza között fennáll a következő összefüggés: \( T=\frac{K}{2}·r_{b} \). Bevezetve az \( s=\frac{K}{2} \) jelölést , háromszög területére a következő összefüggést kapjuk: T=s⋅rb.
Ez könnyen belátható.
A beírt kör „M” középpontja az ABC háromszöget olyan három darab háromszögre bontja (ABM, BMC és a CAM háromszögek), amelyek magassága mindhárom esetben az rb sugár. Ezen háromszögek területei:
\( T_{ABM}=\frac{c·r_{b}}{2} \), \( T_{BCM}=\frac{a·r_{b}}{2} \) , \( T_{CAM}=\frac{b·r_{b}}{2} \).
Ezek összege az eredeti ABC háromszög területe: TABC=TABM+TBCM+TCAM.
\[ T_{ABC}=\frac{c·r_{b}}{2}+\frac{a·r_{b}}{2}+\frac{b·r_{b}}{2}=\frac{(a+b+c)·r_{b}}{2}=\frac{K·r_{b}}{2}=s·r_{b} \]
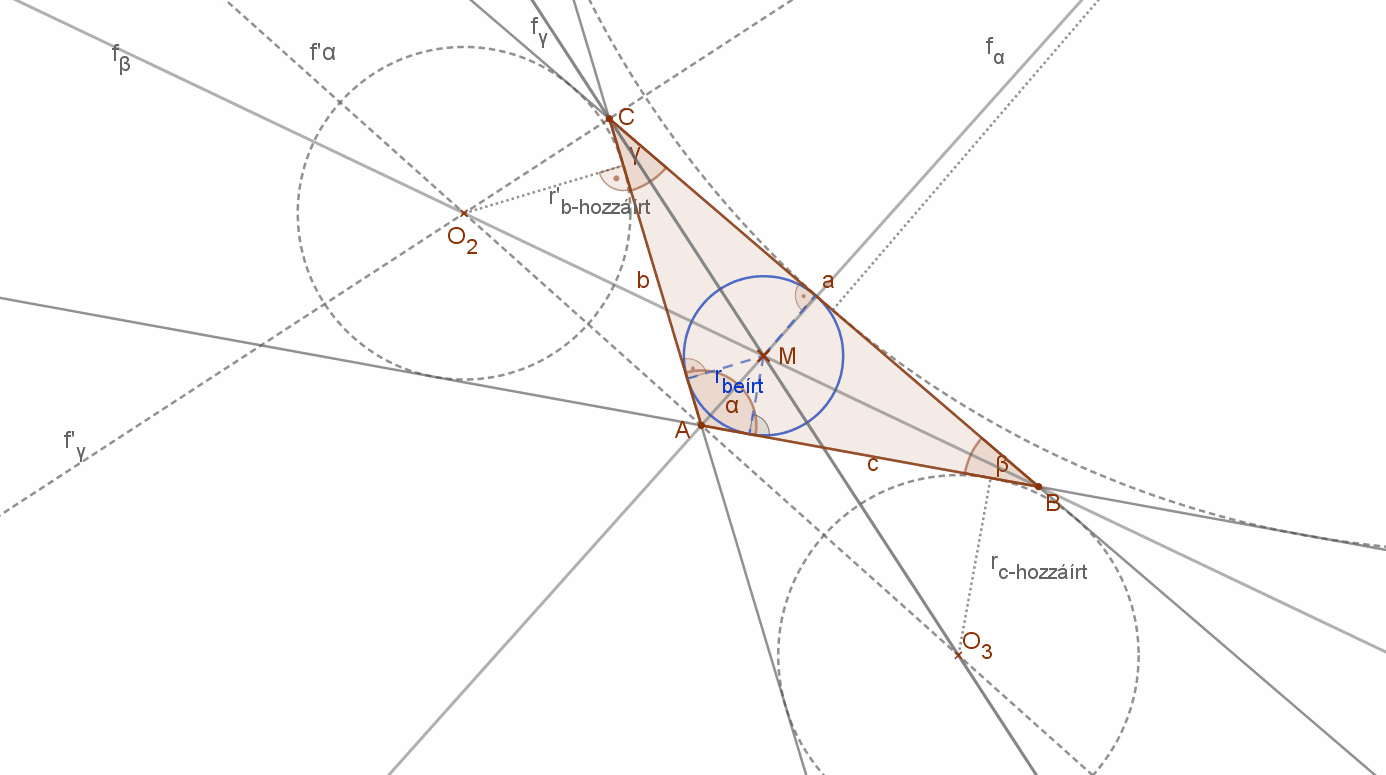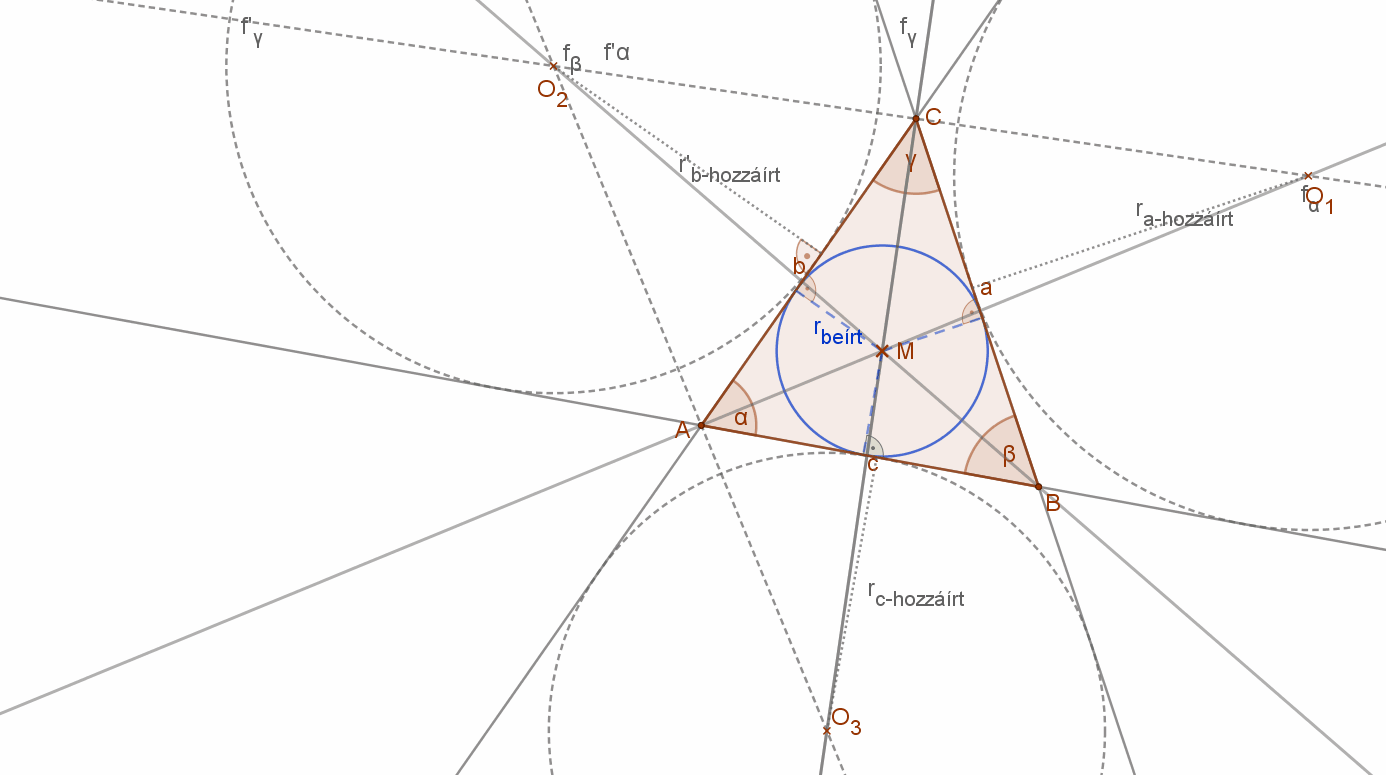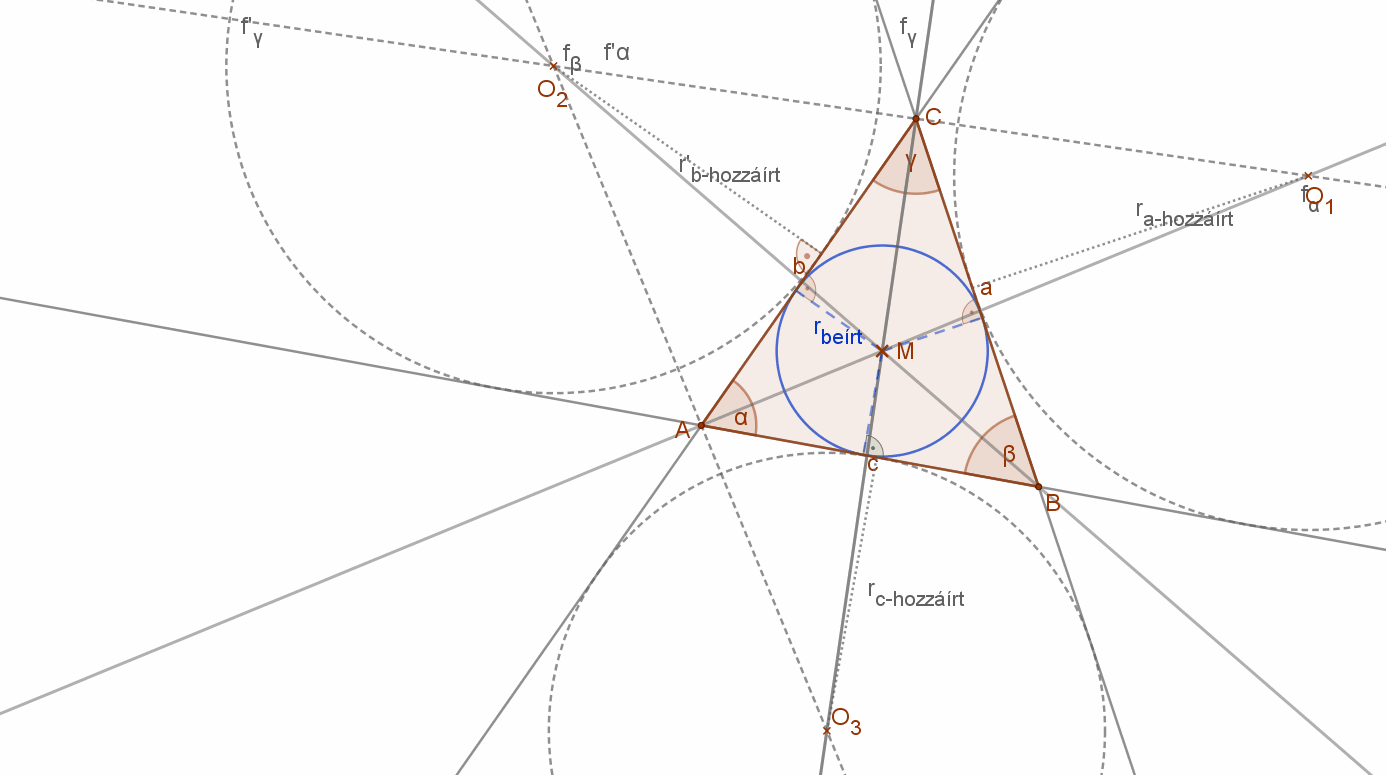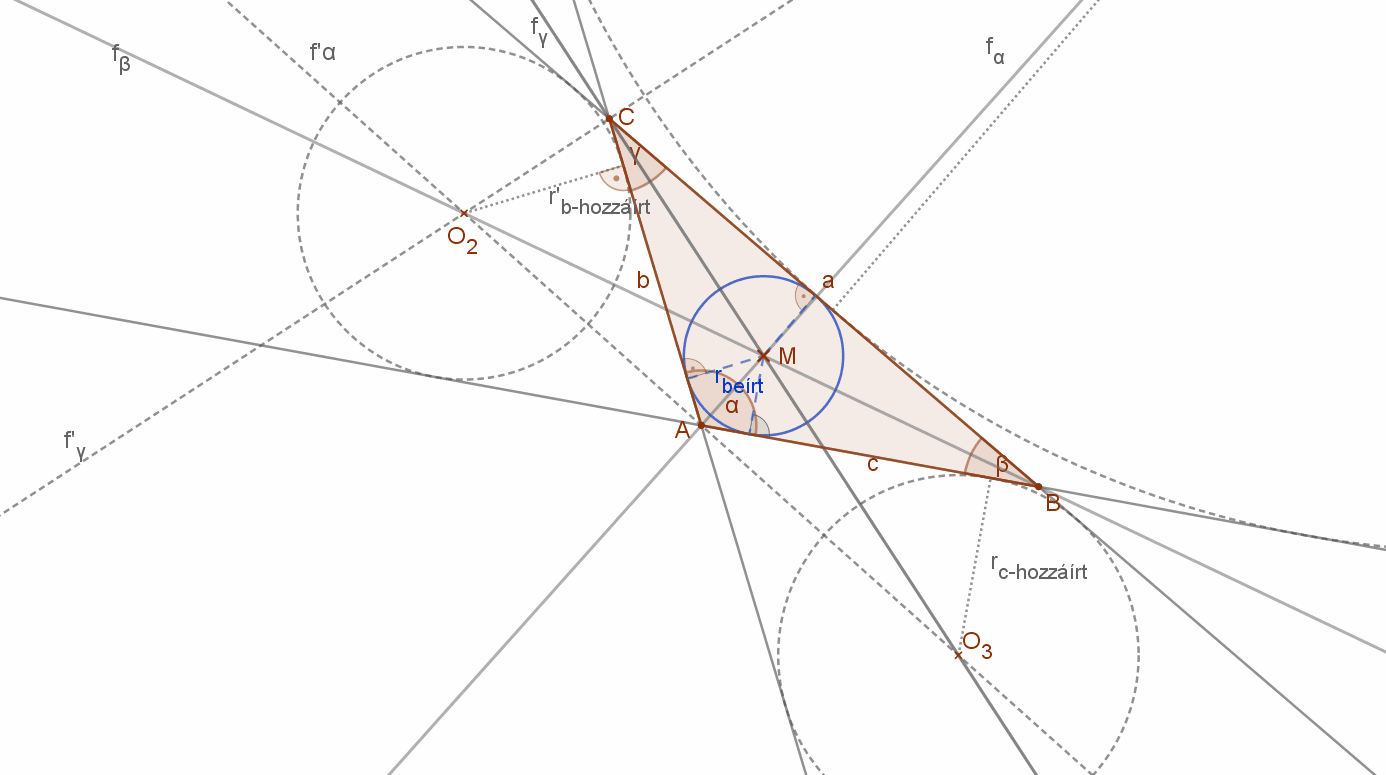
Megjegyzés: A háromszögek egy belső, valamint a nem mellette levő külső szögeinek szögfelezői is egy pontban metszik egymást. Ez a pont a háromszög hozzáírt körének a középpontja, amely kör a háromszög oldalain kívül helyezkedik el és érinti a háromszög oldalait illetve azok meghosszabbításait. Minden háromszögnek tehát egy beírt és három hozzáírt köre van.


Comments are closed, but trackbacks and pingbacks are open.